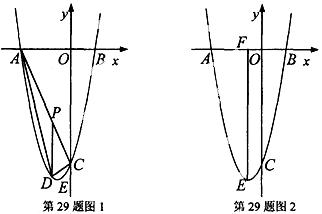
抛物线y＝x2＋bx＋c经过点A(－4，0)，B(2，0)且与y轴交于点C．
(1)求抛物线的解析式；
(2)如图1，P为线段AC上一点，过点P作y轴平行线，交抛物线于点D，当△ADC的面积最大时，求点P的坐标；
(3)如图2，
抛物线顶点为E，EF⊥x轴子F点，M、N分别是x轴和线段EF上的动点，设M的坐标为(m，0)，若∠MNC＝9
0°，请指出实数m的变化范围，并说明理由．
黄冈创优卷系列答案科目：初中数学 来源： 题型：
下列说法不正确的是 ( )
A．某种彩票中奖的概率是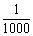
，买1000张该种彩票一定会中奖
B．了解一批电视机的使用寿命适合用抽样调查
C．若甲组数据的标准差S甲=0.31，乙组数据的标准差S乙=0.25，则乙组数据比甲组数据稳定
D．在一个装有白球和绿球的袋中摸球，摸出黑球是不可能事件
查看答案和解析>>
科目：初中数学 来源： 题型：
如图1，已知Rt△ABC中，
，AC＝8cm，BC＝6cm．点P由B出发沿BA方向向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s．以AQ、PQ为
边作平行四边形AQPD，连接DQ，交AB于点E.设运动的时间为t（单位：s）（0≤t ≤4）．解答下列问题：
（1）用含有t的代数式表示AE=_____________．
（2）当t为何值时，DQ=AP．
（3）如图2，当t为何值时，平行四边形AQPD为菱形.
（4）直接写出:当DQ的长最小时，t的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
古希腊著名的毕达哥拉斯学派把1,3，6，10…这样的数称为“三角形数”，而把l、4、9、16．这样的数称为“正方形数”．从图中可以发现，任何一个大于l的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是
A．13=3+10 B．25=9+16
C．36=15+21 D．49=18+31
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
