
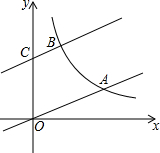
 ��ͼ��ֱ��y=$\frac{1}{3}$x��˫����y=$\frac{k}{x}$��k��0��x��0�����ڵ�A����ֱ��y=$\frac{1}{3}$x����ƽ��3����λ�õ�ֱ��y=ax+b������y�ύ�ڵ�C����˫����y=$\frac{k}{x}$��k��0��x��0�����ڵ�B����OA=2BC��
��ͼ��ֱ��y=$\frac{1}{3}$x��˫����y=$\frac{k}{x}$��k��0��x��0�����ڵ�A����ֱ��y=$\frac{1}{3}$x����ƽ��3����λ�õ�ֱ��y=ax+b������y�ύ�ڵ�C����˫����y=$\frac{k}{x}$��k��0��x��0�����ڵ�B����OA=2BC������ ��1���ֱ����A��B��AD��x�ᣬBE��x�ᣬCF��BE�ڵ�F������A��2x��$\frac{2}{3}$x��������OA=3BC���ʿɵó�B��x��$\frac{1}{3}$x+3�����ٸ��ݷ�����������k=xyΪ��ֵ���k��ֵ���ɣ�
��2���������̣���ý���B�����꣬����ͼ�����ax+b-$\frac{k}{x}$��0ʱx��ȡֵ��Χ��
��� �⣺��1���ֱ����A��B��AD��x�ᣬBE��x�ᣬCF��BE�ڵ�F����A��2x��$\frac{2}{3}$x����
��OA=2BC��BC��OA��CF��x�ᣬ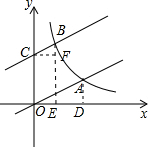
���BCF�ס�AOD��
��CF=$\frac{1}{2}$OD��
�ߵ�B��ֱ��y=$\frac{1}{3}$x+3�ϣ�
��B��x��$\frac{1}{3}$x+3����
�ߵ�A��B��˫����y=$\frac{k}{x}$��k��0��x��0���ϣ�
��2x•$\frac{2}{3}$x=x•��$\frac{1}{3}$x+3�������x=3��
��k=2��3��$\frac{2}{3}$��3=12��
��˫���ߵı���ʽΪy=$\frac{12}{x}$��
��2����$\left\{\begin{array}{l}{y=\frac{1}{3}x+3}\\{y=\frac{12}{x}}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$��
��B��3��4����
��ax+b-$\frac{k}{x}$��0ʱx��ȡֵ��Χ��0��x��3��
���� ���⿼����Ƿ�����������һ�κ����Ľ��㣬�����������������ߣ����A��B��������꣬�ٸ���k=xy���ص��г������DZ���Ĺؼ���


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2.58��103 | B�� | 25.8��104 | C�� | 2.58��105 | D�� | 258��103 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
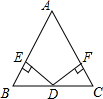 ��֪����ͼ��D�ǡ�ABC��BC�ߵ��е㣬DE��AB��DF��AC������ֱ�ΪE��F����DE=DF����֤��AB=AC��
��֪����ͼ��D�ǡ�ABC��BC�ߵ��е㣬DE��AB��DF��AC������ֱ�ΪE��F����DE=DF����֤��AB=AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3a��3b | B�� | -a��-b | C�� | a+1��b+1 | D�� | $\frac{a}{2}��\frac{b}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com