
【题目】如图甲,对于平面上不大于90°的∠MON,我们给出如下定义:如果点P在∠MON的内部,作PE⊥OM,PF⊥ON,垂足分别为点E、F,那么称PE+PF的值为点P相对于∠MON的“点角距离”,记为d(P,∠MON).如图乙,在平面直角坐标系xOy中,点P在坐标平面内,且点P的横坐标比纵坐标大2,对于∠xOy,满足d(P,∠xOy)=10,点P的坐标是_____.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点E,若DE=3cm,则AC= ( )

A.9cmB.6cmC.12cmD.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记∠AMP=![]() ,∠ONQ=
,∠ONQ=![]() ,当MP+PQ+QN最小时,则
,当MP+PQ+QN最小时,则![]() 与
与![]() 的数量关系是_________________.
的数量关系是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河上有一座桥孔为抛物线形的拱桥,水面宽6m时,水面离桥孔顶部3m.因降暴雨水位上升lm.
(1)如图①,若以桥孔的最高点为原点,建立平面直角坐标系,求抛物线的解析式;
(2)一艘装满物资的小船,露出水面的高为0.5m、宽为4m(横断面如图②).暴雨后这艘船能从这座拱桥下通过吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,∠ABC=90°,AB=BC= ![]() ,三角形的顶点在相互平行的三条直线l1、l2、l3 上,且 l2、l3之间的距离为 2,则 l1、l2 之间的距离为______.
,三角形的顶点在相互平行的三条直线l1、l2、l3 上,且 l2、l3之间的距离为 2,则 l1、l2 之间的距离为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E.(1)求证:△ACD≌△CBE;(2)若BE=5,AD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
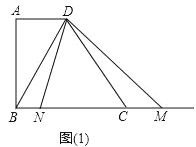
【题目】已知,在梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=4,BC=5,在射线BC任取一点M,联结DM,作∠MDN=∠BDC,∠MDN的另一边DN交直线BC于点N(点N在点M的左侧).
(1)当BM的长为10时,求证:BD⊥DM;
(2)如图(1),当点N在线段BC上时,设BN=x,BM=y,求y关于x的函数关系式,并写出它的定义域;
(3)如果△DMN是等腰三角形,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() .
.![]() 、
、![]() 是边
是边![]() 、
、![]() 边上的动点,
边上的动点,![]() 从
从![]() 出发向
出发向![]() 运动,同时
运动,同时![]() 以相同的速度从
以相同的速度从![]() 出发向
出发向![]() 运动,
运动,![]() 运动到
运动到![]() 停止.
停止.![]() 为
为![]() 中点.
中点.
![]() 试探究
试探究![]() 的形状,并说明理由.
的形状,并说明理由.
![]() 在运动过程中,四边形
在运动过程中,四边形![]() 可能成为正方形吗?如能求正方形的边长.
可能成为正方形吗?如能求正方形的边长.
![]() 当
当![]() 为多少时,
为多少时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com