
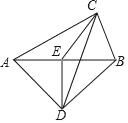
【题目】如图,把一副三角板按如图放置,∠ACB=∠ADB=90°,∠CAB=30°,∠DAB=45°,点E是AB的中点,连结CE,DE,DC.若AB=8,则△DEC的面积为_____.
【答案】4
【解析】
作CF⊥DE交DE的延长线于F,根据直角三角形斜边中线的性质得出DE=CE=AE=BE=![]() AB=4,然后根据∠CAB=30°,∠DAB=45°,得出△BEC是等边三角形,△BDE是等腰直角三角形,即可得出∠CEB=60°,DE⊥AB,进而求得∠ECF=∠CEB=60°,根据30°的直角三角形的性质得出CF=
AB=4,然后根据∠CAB=30°,∠DAB=45°,得出△BEC是等边三角形,△BDE是等腰直角三角形,即可得出∠CEB=60°,DE⊥AB,进而求得∠ECF=∠CEB=60°,根据30°的直角三角形的性质得出CF=![]() CE=2,最后根据三角形面积公式求得即可.
CE=2,最后根据三角形面积公式求得即可.
解:作CF⊥DE交DE的延长线于F,
∵∠ACB=∠ADB=90°,点E是AB的中点,
∴DE=CE=AE=BE=![]() AB=4,
AB=4,
∵∠CAB=30°,∠DAB=45°,
∴△BEC是等边三角形,△BDE是等腰直角三角形,
∴∠CEB=60°,DE⊥AB,
∵CF⊥DE,
∴CF∥AB,
∴∠ECF=∠CEB=60°,
∴CF=![]() CE=2,
CE=2,
∴S△DEC=![]() DECF=
DECF=![]() ×4×2=4,
×4×2=4,
故答案为4.



 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
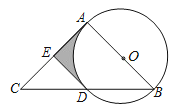
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论错误的是( )
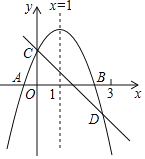
A.2a+b+c>0
B.a<﹣1
C.x(ax+b)≤a+b
D.双曲线y=![]() 的两分支分别位于第一、第三象限
的两分支分别位于第一、第三象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】牧民巴特尔在生产和销售某种奶食品时,采取客户先网上订购,然后由巴特尔付费选择甲或乙快递公司送货上门的销售方式,甲快递公司运送2千克,乙快递公司运送3千克共需运费42元:甲快递公司运送5千克,乙快递公司运送4千克共需运费70元.
(1)求甲、乙两个快递公司每千克的运费各是多少元?
(2)假设巴特尔生产的奶食品当日可以全部出售,且选择运费低的快递公司运送,若该产品每千克的生产成本y1元(不含快递运费),销售价y2元与生产量x千克之间的函数关系式为:y1=![]() ,y2=﹣6x+120(0<x<13),则巴特尔每天生产量为多少千克时获得利润最大?最大利润为多少元?
,y2=﹣6x+120(0<x<13),则巴特尔每天生产量为多少千克时获得利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,半径为1的
中,半径为1的![]() 与
与![]() 轴正半轴和
轴正半轴和![]() 轴正半轴分别交于
轴正半轴分别交于![]() 两点,直线
两点,直线![]() :
:![]() 与
与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 两点.
两点.

(l)当直线![]() 与
与![]() 相切时,求出点
相切时,求出点![]() 的坐标和点
的坐标和点![]() 的坐标;
的坐标;
(2)如图2,当点![]() 在线段
在线段![]() 上时,直线
上时,直线![]() 与
与![]() 交于
交于![]() 两点(点
两点(点![]() 在点
在点![]() 的上方),过点
的上方),过点![]() 作
作![]() 轴,与
轴,与![]() 交于另一点
交于另一点![]() ,连结
,连结![]() 交
交![]() 轴于点
轴于点![]() .
.
①如图3,若点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长并写出解答过程;
的长并写出解答过程;
②如图2,若点![]() 与点
与点![]() 不重合时,
不重合时,![]() 的长是否发生变化,若不发生变化,请求出
的长是否发生变化,若不发生变化,请求出![]() 的长并写出解答过程;若发生变化,请说明理由.
的长并写出解答过程;若发生变化,请说明理由.
(3)如图4,在(2)的基础上,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() ,若点
,若点![]() 在
在![]() 的延长线时,请用等式直接表示线段
的延长线时,请用等式直接表示线段![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实行垃圾资源化利用,是社会文明水平的一个重要体现.某环保公司研发的甲、乙两种智能设备可利用最新技术将干垃圾变身为燃料棒.某垃圾处理厂从环保公司购入以上两种智能设备,若干已知购买甲型智能设备花费360万元,购买乙型智能设备花费480万元,购买的两种设备数量相同,且两种智能设备的单价和为140万元.
(1)求甲乙两种智能设备单价;
(2)垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的40%,且生产每吨燃料棒所需人力成本比物资成本的![]() 倍还多10元,调查发现:若燃料棒售价为每吨200元,平均每天可售出350吨,而当销售价每降低1元,平均每天可多售出5吨,但售价在每吨200元基础上降价幅度不超过7%,
倍还多10元,调查发现:若燃料棒售价为每吨200元,平均每天可售出350吨,而当销售价每降低1元,平均每天可多售出5吨,但售价在每吨200元基础上降价幅度不超过7%,
①垃圾处理厂想使这种燃料棒的销售利润平均每天达到36080元,求每吨燃料棒售价应为多少元?
②每吨燃料棒售价应为多少元时,这种燃料棒平均每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
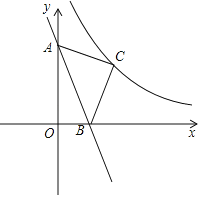
【题目】如图,在平面直角坐标系中,将直线y=﹣3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数y=![]() (x>0)的图象经过点C,求此反比例函数的表达式.
(x>0)的图象经过点C,求此反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某核桃种植基地计划种植![]() 、
、![]() 两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.设该基地种植了
两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.设该基地种植了![]() 种核桃
种核桃![]() 亩.
亩.
(Ⅰ)若该基地收获两种核桃的年总产量为25 800千克,则![]() 、
、![]() 两种核桃各种植了多少亩?
两种核桃各种植了多少亩?
(Ⅱ)全部收购后,总收入为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式.若要求种植
之间的函数关系式.若要求种植![]() 种核桃的面积不少于
种核桃的面积不少于![]() 种核桃的一半,那么种植
种核桃的一半,那么种植![]() 种核桃多少亩时,该种植基地的总收入最多?最多是多少元?
种核桃多少亩时,该种植基地的总收入最多?最多是多少元?
解:(Ⅰ)先用含![]() 的代数式填空,再完成解答.
的代数式填空,再完成解答.
由种植了![]() 种核桃
种核桃![]() 亩,可知
亩,可知![]() 种核桃种植的亩数为________,则
种核桃种植的亩数为________,则![]() 种核桃的年总产量为________千克,
种核桃的年总产量为________千克,![]() 种核桃的年总产量为________千克.
种核桃的年总产量为________千克.
根据题意列出方程________________________;
解得:
(Ⅱ)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com