
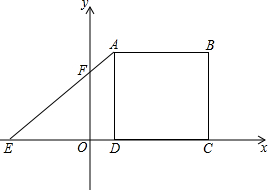
 如图,在平面直角坐标系中,点O为坐标原点,点A(x,y)中的横坐标x与纵坐标y满足$\sqrt{x-2}$+|y-8|=0,过点A作x轴的垂线,垂足为点D,点E在x轴的负半轴上,且满足AD-OD=OE,线段AE与y轴相交于点F,将线段AD向右平移8个单位长度,得到线段BC.
如图,在平面直角坐标系中,点O为坐标原点,点A(x,y)中的横坐标x与纵坐标y满足$\sqrt{x-2}$+|y-8|=0,过点A作x轴的垂线,垂足为点D,点E在x轴的负半轴上,且满足AD-OD=OE,线段AE与y轴相交于点F,将线段AD向右平移8个单位长度,得到线段BC.分析 (1)根据非负性得出点A的坐标,进而求出OD,AD,OE,即可得出点E的坐标;
(2)先求出AB,CE,BC,再用三角形的面积公式列方程即可求出CG,
(3)先由运动得出PC,CQ,进而表示出OP,GQ,再用面积的差表示出三角形PFG和三角形FGQ的面积,进而建立方程求解即可得出点P的坐标.
解答 解:(1)∵$\sqrt{x-2}$+|y-8|=0,
∴x=2,y=8,
∴A(2,8),
∴OD=2,AD=8,
∵AD-OD=OE,
∴OE=8-2=6,
∴E(-6,0),
故答案为:2,8;-6,0;
(2)如图1, 由平移得,BC=AD=8,
由平移得,BC=AD=8,
∴BG=BC-CG=8-CG,AB=CD=8,
∴CE=OD+CD+OE=16,
∵三角形ABG的面积与三角形EGC的面积的和为40,
∴S△ABG+S△EGC=$\frac{1}{2}$BG×AB+$\frac{1}{2}$CG×CE=$\frac{1}{2}$×(8-CG)×8+$\frac{1}{2}$CG×16=40,
∴CG=2,
(3)如图2,由(2)知,OC=8,OD=2,AD=8,OE=6,
∴DE=8,
∵OF∥AD,
∴$\frac{OE}{ED}=\frac{OF}{AD}$,
∴$\frac{6}{8}=\frac{OF}{8}$,
∴OF=6, 设点P,Q同时运动t秒钟,三角形FGP的面积是三角形FGQ的面积的2倍,
设点P,Q同时运动t秒钟,三角形FGP的面积是三角形FGQ的面积的2倍,
∴PC=2t,CQ=t(0≤t≤5),
∴OP=OC-PC=10-2t,GQ=|t-2|
∴S△PFG=S梯形FOCG-S△POF-S△PCG
=$\frac{1}{2}$(CG+OF)×OC-$\frac{1}{2}$OP×OF-$\frac{1}{2}$PC×CG
=$\frac{1}{2}$×(2+6)×10-$\frac{1}{2}$×(10-2t)×6-$\frac{1}{2}$×2t×2
=4t+10,
S△FGQ=$\frac{1}{2}$GQ×OC=$\frac{1}{2}$|t-2|×10=5|t-2|,
∵三角形FGP的面积是三角形FGQ的面积的2倍,
∴4t+10=2×5|t-2|,
①当t>2时,t-2>0,点Q在BG上,4t+10=2×5(t-2)
∴t=5,
∴OP=0,
∴P(0,0)
②当t<2时,t-2<0,点Q在CG上,4t+10=2×5(2-t),
∴t=$\frac{5}{7}$
∴OP=10-2t=$\frac{60}{7}$,
∴P($\frac{60}{7}$,0),
∴点P的坐标为(0,0)或($\frac{60}{7}$,0).
点评 此题是三角形综合题,主要考查了非负性,线段的计算,三角形,梯形的面积公式,平移的性质,解本题的关键是掌握三角形的面积的计算方法,是一道比较简单的综合题.


科目:初中数学 来源: 题型:选择题
| A. | (-$\sqrt{5}$)2=-5 | B. | $\sqrt{(-0.5)^{2}}$=-0.5 | C. | (-$\sqrt{5}$)2=52 | D. | $\sqrt{(-0.5)^{2}}$=0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 58.9×104 | B. | 5.89×105 | C. | 5.89×104 | D. | 0.589×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
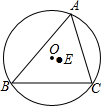 在△ABC内接于半径为2的⊙O,∠BAC=60°,△ABC的内心为E,当点A在优弧$\widehat{BAC}$上运动时,则点E运动的路径长为( )
在△ABC内接于半径为2的⊙O,∠BAC=60°,△ABC的内心为E,当点A在优弧$\widehat{BAC}$上运动时,则点E运动的路径长为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com