
【题目】如图,己知△ABC是等边三角形,点P在△ABC内,点Q在△ABC外,分别连接AP、BP、AQ、CQ,∠ABP=∠ACQ, BP=CQ.
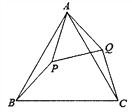
(1)求证:△ABP≌△ACQ;
(2)连接PQ,求证△APQ是等边三角形;
(3)连接P设△CPQ是以![]() PQC为顶角的等腰三角形,且∠BPC=100
PQC为顶角的等腰三角形,且∠BPC=100![]() ,求∠APB的度数.
,求∠APB的度数.
【答案】(1)答案见解析;(2)答案见解析;(3)160°
【解析】试题分析:易证AB=AC,∠BAC=60°,即可证明△ABP≌△ACQ,可得∠BAP=∠CAQ,AP=AQ,即可求得∠PAQ=60°,即可解题.
(1)证明: ∵ △ABC是等边三角形,
∴ AB=AC .
在△ABP和△ACQ中
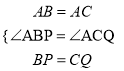 ,
,
∴ △ABP ≌ △ACQ ( SAS ).
(2)证明: ∵ △ABP ≌ △ACQ,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∵ △ABC是等边三角形,
∴ ![]() ,
,
∴ ![]() ,
,
∴ △APQ是等边三角形.
(3)解: 如图示
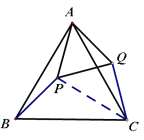
∵ △CPQ是等腰三角形,∠PQC为顶角,
∴ ![]() .
.
设![]() ,
,
![]() =
=![]() .
.
∵ △APQ是等边三角形,
∴ ![]() ,
,
∴ ![]() .
.
∵ △ABP ≌ △ACQ,
∴ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
又∵ ![]()
∴ ![]() ,
,
解得 ![]() ,
,
∴ ![]() .
.
点睛: 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了正三角形的判定,本题中求证△ABP≌△ACQ是解题的关键.


科目:初中数学 来源: 题型:
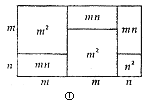
【题目】有许多代数恒等式可以用图形的面积来表示,如图①,它表示(2m+n)(m+n)=2m2+3mn+n2.
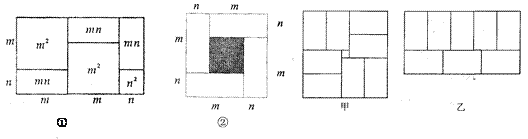
(1) 观察图②,请你写出三个代数式(m+n) 2、(m-n) 2、mn之间的等量关系是_________;
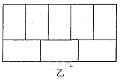
(2) 小明用8个一样大的长方形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,图案乙是一个大的长方形:图案甲的中间留下了边长是2cm的正方形小洞.则(a+2b)2-8ab的值_______.


查看答案和解析>>
科目:初中数学 来源: 题型:
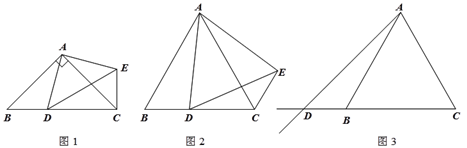
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.(1)甲蚂蚁选择“向左”爬行的概率为________;
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,已知直线![]() 和双曲线
和双曲线![]() (k>0),点A(m,n)在双曲线
(k>0),点A(m,n)在双曲线 ![]() 上.当m=n=2时.
上.当m=n=2时.
(1)直接写出k的值;
(2)将直线![]() 作怎样的平移能使平移后的直线与双曲线
作怎样的平移能使平移后的直线与双曲线 ![]() 只有一个交点.
只有一个交点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△DEF是由△ABC绕点O顺时针旋转180°后形成的图形;
(1)请你指出图中所有相等的线段;
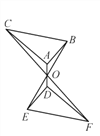
(2)图中哪些三角形可以被看成是关于点O成中心对称关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点A,点B(1,0),与
轴交于点A,点B(1,0),与![]() 轴交于点C(0,﹣3),点M是其顶点.
轴交于点C(0,﹣3),点M是其顶点.
(1)求抛物线解析式;
(2)第一象限抛物线上有一点D,满足∠DAB=45°,求点D的坐标;
(3)直线![]() (﹣3<
(﹣3<![]() <﹣1)与x轴相交于点H.与线段AC,AM和抛物线分别相交于点E,F,P.证明线段HE,EF,FP总能组成等腰三角形.
<﹣1)与x轴相交于点H.与线段AC,AM和抛物线分别相交于点E,F,P.证明线段HE,EF,FP总能组成等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(![]() )如图①,已知正方形
)如图①,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 和
和![]() 分别是边
分别是边![]() 、
、![]() 上两点,且
上两点,且![]() .连接
.连接![]() 和
和![]() ,交于点
,交于点![]() .猜想
.猜想![]() 与
与![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(![]() )如图②,已知正方形
)如图②,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 和
和![]() 分别从点
分别从点![]() 、
、![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 、
、![]() 方向向终点
方向向终点![]() 和
和![]() 运动,连接
运动,连接![]() 和
和![]() ,交于点
,交于点![]() ,求
,求![]() 周长的最大值.
周长的最大值.
问题解决
(![]() )如图③,
)如图③,![]() 为边长为
为边长为![]() 的菱形
的菱形![]() 的对角线,
的对角线, ![]() .点
.点![]() 和
和![]() 分别从点
分别从点![]() 、
、![]() 同时出发;以相同的速度沿
同时出发;以相同的速度沿![]() 、
、![]() 向终点
向终点![]() 和
和![]() 运动,连接
运动,连接![]() 和
和![]() ,交于点
,交于点![]() ,求
,求![]() 周长的最大值.
周长的最大值.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com