
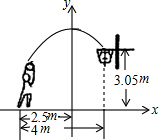
 如图,运动员甲在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
如图,运动员甲在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.分析 (1)设抛物线的表达式为y=ax2+3.5,依题意可知图象经过的坐标,由此可得a的值.
(2)设球出手时,他跳离地面的高度为hm,则可得h+2.05=-0.2×(-2.5)2+3.5.
(3)当y=3.3m,进而代入函数解析式,求出x的值,即可得出答案.
解答 解:(1)∵当球运行的水平距离为2.5米时,达到最大高度3.5米,
∴抛物线的顶点坐标为(0,3.5),
∴设抛物线的表达式为y=ax2+3.5.
由图知图象过以下点:(1.5,3.05).
∴2.25a+3.5=3.05,
解得:a=-0.2,
∴抛物线的表达式为y=-0.2x2+3.5.
(2)设球出手时,他跳离地面的高度为hm,
因为(1)中求得y=-0.2x2+3.5,
则球出手时,球的高度为h+1.8+0.25=(h+2.05)m,
∴h+2.05=-0.2×(-2.5)2+3.5,
∴h=0.2(m).
答:球出手时,他跳离地面的高度为0.2m.
(3)由题意可得出:y=3.3,
则3.3=-0.2x2+3.5
解得:x1=1,x2=-1,
∴4-1=3(m),
∴乙在距离甲3米范围内或离篮板0.5米的范围内能在空中截住球.
点评 此题主要考查了二次函数的应用,建立合适的平面直角坐标系是解决本题的突破点,求得球出手时距离地面的高度是解决本题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com