
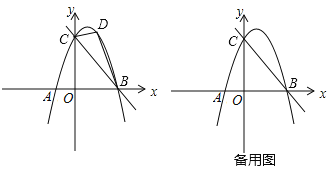
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与![]() 轴相交于A、B两点,与
轴相交于A、B两点,与![]() 轴相交于点C,OA=1,OC=3,连接BC.
轴相交于点C,OA=1,OC=3,连接BC.
(1)求b的值;
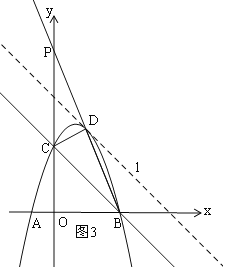
(2)点D是直线BC上方抛物线一动点(点B、C除外),当△BCD的面积取得最大值时,在![]() 轴上是否存在一点P,使得|PB﹣PD|最大,若存在,请求出点P的坐标;若不存在,请说明理由.
轴上是否存在一点P,使得|PB﹣PD|最大,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,若在平面上存在点Q,使得以点B、C、D、Q为顶点的四边形为平行四边形,请直接写出点Q坐标.
【答案】(1)b=2,c=3;(2)P(0,![]() );(3) (-
);(3) (-![]() ,
,![]() ),(
),(![]() ,-
,-![]() ),(
),(![]() ,
,![]() ),
),
【解析】
(1)根据OA=1,OC=3得出点A和C的坐标,代入抛物线的解析式列方程组可得b的值;(2)写出抛物线的解析式,利用三角形面积公式可知,当底边BC一定时,高最大时其△BCD的面积最大,即作BC的平行线,其平行线的距离最大时,即平行线l与抛物线有一个交点时,交点为D,利用方程组的解可得D的坐标,最后根据三角形的三边关系确定当P、B、D三点共线时,|PB﹣PD|最大,利用待定系数法求直线BD的解析式,与y轴的交点就是点P;(3)如图4,画出平行四边形,有三种情况:根据平移规律确定Q的坐标.
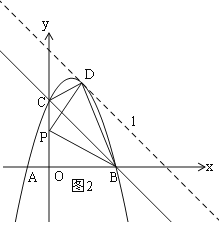
(1)∵OA=1,OC=3,
∴A(-1,0),C(0,3),
把A(-1,0),C(0,3)代入抛物线y=-x2+bx+c中得:
∵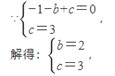 ,
,
(2)由(1)得:抛物线y=-x2+2x+3,
当y=0时,-x2+2x+3=0,
解得:x=-1或3,
∴B(3,0),
设直线BC的解析式为:y=kx+b,
 ,
,
∴直线BC的解析式为:y=-x+3,
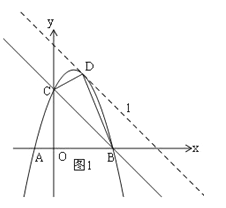
如图1,作直线l∥BC,
设直线l的解析式为:y=-x+b,
由题意可知:△BCD中边BC长一定,当△BCD的面积取得最大值时,即以BC为底边,其高最大,
也就是直线l与抛物线有一个交点时,三角形高最大,△BCD的面积最大,
则![]() ,
,
-x2+2x+3=-x+b,
x2-3x+b-3=0,
△=(-3)2-4×1×(b-3)=0, ,
,
∵P是y轴上任意一点,
如图2,|PB-PD|<BD,
∴当P、B、D三点共线时,|PB-PD|最大,如图3,
(3)如图4,分三种情况:
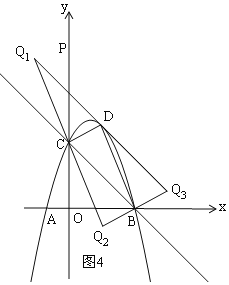
①当CD为平行四边形的对角线时,


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
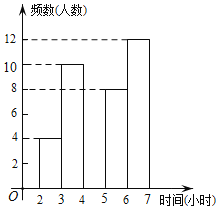
【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )

A.x+y=7B.x﹣y=2C.x2﹣y2=4D.4xy+4=49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数![]() 的图象交于第二、四象限内的A,B两点,与
的图象交于第二、四象限内的A,B两点,与![]() 轴交于C点,过点A作AH⊥
轴交于C点,过点A作AH⊥![]() 轴,垂足为H,OH=3,tan∠AOH=
轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(
,点B的坐标为(![]() ,﹣2).
,﹣2).
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
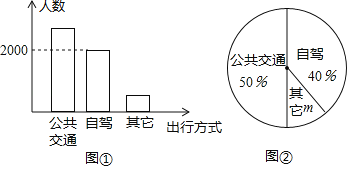
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对称中心在坐标原点,AB∥x轴,AD、BC分别与x轴交于E、F,连接BE、DF,若正方形ABCD有两个顶点在双曲线y=![]() 上,实数a满足a3﹣a=1,则四边形DEBF的面积是_____.
上,实数a满足a3﹣a=1,则四边形DEBF的面积是_____.
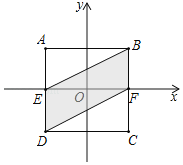
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△ADE均为等边三角形,点O是AC的中点,点D在射线BO上,连结OE,EC,则∠ACE=_____°;若AB=1,则OE的最小值=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现问题)
如图1,已知![]() ,以点
,以点![]() 为直角顶点,
为直角顶点,![]() 为腰向
为腰向![]() 外作等腰直角
外作等腰直角![]() 、请你以
、请你以![]() 为直角顶点、
为直角顶点、![]() 为腰,向
为腰,向![]() 外作等腰直角
外作等腰直角![]() (不写作法,保留作图痕迹).连接
(不写作法,保留作图痕迹).连接![]() 、
、![]() .那么
.那么![]() 与
与![]() 的数量关系是________.
的数量关系是________.
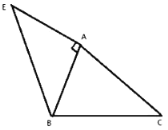
(拓展探究)
如图2,已知![]() ,以
,以![]() 、
、![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]() 、
、![]() ,试判断
,试判断![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.

(解决问题)
如图3,有一个四边形场地![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
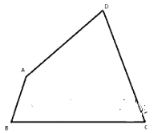
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com