
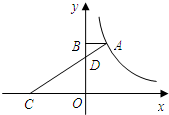
 如图,A是反比例函数y=$\frac{k}{x}$(k≠0)的图象上一点,点B、D在y轴正半轴上,△ABD是COD关于点D的位似图形,且△ABD与△COD的位似比为1:3,△ABD的面积为1,试求该反比例函数的解析式.
如图,A是反比例函数y=$\frac{k}{x}$(k≠0)的图象上一点,点B、D在y轴正半轴上,△ABD是COD关于点D的位似图形,且△ABD与△COD的位似比为1:3,△ABD的面积为1,试求该反比例函数的解析式. 分析 根据△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,得出$\frac{CQ}{CE}$=$\frac{DO}{AE}$=$\frac{3}{4}$,进而得出假设BD=x,AE=4x,D0=3x,AB=y,根据△ABD的面积为1,求出xy=2即可得出答案.
解答 解:过A作AE⊥x轴,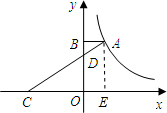
∵△ABD是△COD关于点D的位似图形,
且△ABD与△COD的位似是1:3,
∴$\frac{CO}{AB}$=$\frac{1}{3}$,
∴OE=AB,
∴$\frac{CQ}{CE}$=$\frac{DO}{AE}$=$\frac{3}{4}$,
设BD=x,AB=y
∴DO=3x,AE=4x,C0=3y,
∵△ABD的面积为1,
∴$\frac{1}{2}$xy=1,
∴xy=2,
∴AB•AE=4xy=8,
该反比例函数的表达式为:y=$\frac{8}{x}$.
点评 此题主要考查了位似图形的性质以及反比例函数的综合应用,得出假设BD=x,AE=4x,D0=3x,AB=y,根据△ABD的面积为1,求出xy=2是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )
如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为( )| A. | 10 m | B. | 15 m | C. | 18 m | D. | 20 m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A | B. | ∠A或∠B | C. | ∠C | D. | ∠B或∠C |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com