
分析 分别令x=0和y=0代入求抛物线与两坐标轴的交点,写出相应线段的长,再证明△AOC∽△COB,$\frac{AO}{OC}=\frac{OC}{OB}$,代入即可求出m的值,并取舍.
解答  解:如图,当x=0时,y=2m+5,
解:如图,当x=0时,y=2m+5,
∴C(0,2m+5),
∴OC=2m+5,
当y=0时,-$\frac{1}{2}$x2+mx+2m+5=0,
x2-2mx-4m-10=0,
x=m±$\sqrt{{m}^{2}+4m+10}$,
∴A(m-$\sqrt{{m}^{2}+4m+10}$,0)、B(m+$\sqrt{{m}^{2}+4m+10}$,0),
∴OB=m+$\sqrt{{m}^{2}+4m+10}$,OA=-m+$\sqrt{{m}^{2}+4m+10}$,
∵△ABC是直角三角形,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
∵∠BOC=90°,
∴∠BCO+∠OBC=90°,
∴∠ACO=∠OBC,
∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴$\frac{AO}{OC}=\frac{OC}{OB}$,
∴OC2=AO•OB,
∴(2m+5)2=(m+$\sqrt{{m}^{2}+4m+10}$)(-m+$\sqrt{{m}^{2}+4m+10}$),
4m2+20m+25=m2+4m+10-m2,
4m2+16m+15=0,
(2m+3)(2m+5)=0,
m1=-$\frac{3}{2}$,m2=-$\frac{5}{2}$,
当m2=-$\frac{5}{2}$时,y=-$\frac{1}{2}{x}^{2}$-$\frac{5}{2}$x,
此时抛物线与y轴交在原点处,即抛物线与两坐标轴的交点为两个,不能构建成三角形,不符合题意,舍去;
∴m=-$\frac{3}{2}$,
故答案为:-$\frac{3}{2}$.
点评 本题考查了抛物线与两坐标轴的交点,与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.与y轴的交点,令x=0,即y=c;根据直角三角形,证明两三角形相似,列比例式可求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
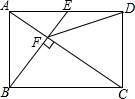 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠ACD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}{S_{△ABF}}$其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠ACD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}{S_{△ABF}}$其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com