
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,与过
,与过![]() 点的直线相交于另一点
点的直线相交于另一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .
.

(1)求抛物线的解析式.
(2)点![]() 是
是![]() 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
①若点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,求
,求![]() 面积的最大值.
面积的最大值.
②设![]() 的长为
的长为![]() ,是否存在
,是否存在![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在,当
;②存在,当![]() 时,以点
时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
【解析】
(1)把![]() ,
,![]() 带入
带入![]() 即可求得解析式;
即可求得解析式;
(2)先用含m的代数式表示点P、M的坐标,再根据三角形的面积公式求出PCM的面积和m的函数关系式,然后求出PCM的最大值;
(3)由平行四边形的性质列出关于t的一元二次方程,解方程即可得到结论
解:(1)∵抛物线![]() 过点
过点![]() 、点
、点![]() ,
,
∴ 解得
解得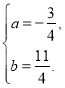
∴抛物线的解析式为![]() .
.
(2)∵抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴可知![]() 点坐标为
点坐标为![]() .
.
∴可设直线![]() 的解析式为
的解析式为![]() .
.
把点![]() 代人
代人![]() 中,得
中,得![]() ,
,
∴![]() .
.
∴直线![]() 的解析式为
的解析式为![]() .
.
①∵![]() 轴,
轴,
∴![]() .
.
设![]() ,则
,则![]() ,且
,且![]() .
.
∴![]() ,
,
∴![]() .
.
∴ .
.
∴当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.
②存在.
由题可知![]() ,
,![]() .
.
∴当![]() 时,以点
时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
已知![]() 的长为
的长为![]() ,所以
,所以![]() ,
,![]() .
.
∴![]() .
.
∴当![]() 时,
时,
解得![]() (不符合题意,舍去),
(不符合题意,舍去),![]() ;
;
当![]() 时,
时, ,
,
∴此方程无实数根.
综上,当![]() 时,以点
时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为![]() 的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为
的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为![]() ,种草所需费用
,种草所需费用![]() (元)与
(元)与![]() 的函数关系式为
的函数关系式为 ,其大致图象如图所示.栽花所需费用
,其大致图象如图所示.栽花所需费用![]() (元)与
(元)与![]() 的函数关系式为
的函数关系式为![]() .
.

(1)求出![]() ,
,![]() 的值;
的值;
(2)若种花面积不小于![]() 时的绿化总费用为
时的绿化总费用为![]() (元),写出
(元),写出![]() 与
与![]() 的函数关系式,并求出绿化总费用
的函数关系式,并求出绿化总费用![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(2,1),B(-1,
的图象交于A(2,1),B(-1,![]() )两点.
)两点.
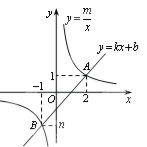
(1)求m、k、b的值;
(2)连接OA、OB,计算三角形OAB的面积;
(3)结合图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣4x2﹣8mx﹣m2+2m的顶点p.
(1)点p的坐标为 (含m的式子表示)
(2)当﹣1≤x≤1时,y的最大值为5,则m的值为多少;
(3)若抛物线与x轴(不包括x轴上的点)所围成的封闭区域只含有1个整数点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;

(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;

(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与反比例函数y=
x+3的图象与反比例函数y=![]() (x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(x>0,k是常数)的图象交于A(a,2),B(4,b)两点.
(1)求反比例函数的表达式;
(2)点C是第一象限内一点,连接AC,BC,使AC∥x轴,BC∥y轴,连接OA,OB.若点P在y轴上,且△OPA的面积与四边形OACB的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A.
(a>0,b<0)的图象与x轴只有一个公共点A.
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)求A点的坐标(只含b的代数式来表示);
(3)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,2),B(0,-2)其对称轴为直线x=![]() ,C(0,
,C(0, ![]() )为y轴上一点,直线AC与抛物线交于另一点D,
)为y轴上一点,直线AC与抛物线交于另一点D,
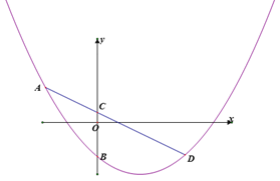
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点F使△ADF是直角三角形,如果存在,求出点F的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a= ![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有三个.其中正确的结论是( )
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有三个.其中正确的结论是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com