练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
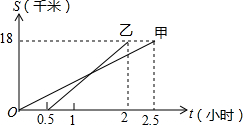
    8．甲、乙两同学从A地出发，骑自行车在同一条路上行驶到距A地18千米的B地，他们离开A地的距离S（千米）和行驶时间t（小时）之间的函数关系图象如图所示，根据题目和图象所提供的信息，下列说法正确的是（　　）
    A．乙比甲先到达B地B．乙在行驶过程中没有追上甲
    C．乙比甲早出发半小时D．甲的行驶速度比乙的行驶速度快

    分析 由图象可知，根据甲乙到达终点的时间，判断A；两条线段相交，说明乙在行驶过程中追上甲，判断B；甲比乙先出发0.5小时，判断C；甲乙行驶的时间，路程来计算速度，判断D．

    解答 解：A、由于S=18时，t甲=2.5，t乙=2，所以乙比甲先到达B地，故本选项说法正确；
    B、由于甲与乙所表示的S与t之间的函数关系的图象由交点，且交点的横坐标小于2，所以乙在行驶过程中追上了甲，故本选项说法错误；
    C、由于S=0时，t甲=0，t乙=0.5，所以甲同学比乙同学先出发半小时，故本选项说法错误；
    D、根据速度=路程÷时间，可知甲的行驶速度为18÷2.5=7.2千米/时，乙的行驶速度为18÷1.5=12千米/时，所以甲的行驶速度比乙的行驶速度慢，故本选项说法错误；
    故选：A．

    点评 此题考查了函数的图象及学生从图象中读取信息的数形结合能力．解决此类识图题，同学们要注意分析其中的“关键点”，还要善于分析各图象的变化趋势．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．随着“中国最美高铁线”--京福高铁的通车，在此铁路线上的A地到B地更为方便、快捷．下面是从A地至B地乘坐高铁与普遍列车的三条信息；
    ①从A地至B地高铁的行驶时间比普通列车少$\frac{2}{3}$小时；
    ②A地至B地的高铁线大约有70km，普通列车线的路线是高铁的1.2倍；
    ③高铁的平均行驶速度是普通列车的2.5倍；
    请你根据上面的信息，求出从A地至B地高铁的平均行驶速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．先阅读下列材料，再解决问题：
    阅读材料：数学上有一种根号内又带根号的数，它们能通过完全平方公式及二次根式的性质化去一层根号．
    例如：$\sqrt{3+2\sqrt{2}}$=$\sqrt{3+2×1×\sqrt{2}}$=$\sqrt{{1}^{2}+（\sqrt{2}）^{2}+2×1×\sqrt{2}}$=$\sqrt{（1+\sqrt{2}）^{2}}$=|1+$\sqrt{2}$|=1+$\sqrt{2}$
    解决问题：
    ①模仿上例的过程填空：
    $\sqrt{14+6\sqrt{5}}$=$\sqrt{14+2×3×\sqrt{5}}$=$\sqrt{{3}^{2}+2×3×\sqrt{5}+（\sqrt{5}）^{2}}$=$\sqrt{（3+\sqrt{5}）^{2}}$=|3+$\sqrt{5}$|=3+$\sqrt{5}$
    ②根据上述思路，试将下列各式化简．
    （1）$\sqrt{28-10\sqrt{3}}$              （2）$\sqrt{1+\frac{{\sqrt{3}}}{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，已知△ABC内接于⊙O，AD为边上的高，将△ADC沿直线AC翻折得到△AEC，延长EA交⊙O于点P，连接FC，交AB于N．
    （1）求证：∠BAC=∠ABC+∠ACF；
    （2）求证：EF=DB；
    （3）若AD=5，CD=10，CB∥AF，求点F到AB的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

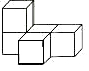    3．如图所示的几何体是由五个完全相同且棱长为1的正方体组成的，下列关于这个几何体的说法正确的是（　　）
    A．主视图的面积为5B．俯视图的面积为3
    C．左视图的面积为3D．三个视图的面积都为4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．已知a+b=2，则a2+4b-b2的值是（　　）
    A．4B．3C．2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列计算正确的是（　　）
    A．（a-b）2=a2-b2B．（2a+b）（-2a+b）=2a2-b2
    C．（a+1）（a-2）=a2-2D．（-a-b）2=a2+2ab+b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

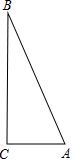    17．实践操作：如图，△ABC是直角三角形，∠ACB=90°，利用直尺和圆规按下列要求作图，并在图中标明相应的字母．（保留作图痕迹，不写作法）
    ①作∠BAC的平分线，交BC于点O；
    ②以点O为圆心，OC为半径作圆．
    综合运用：在你所作的图中，
    （1）直线AB与⊙O的位置关系是相切；
    （2）证明：BA•BD=BC•BO；
    （3）若AC=5，BC=12，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

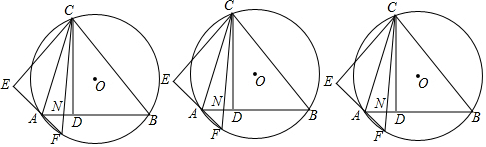
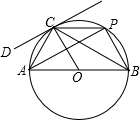    18．如图，点C是半径长为3的⊙O上任意一点，AB为直径，AC=3，过点C作⊙O的切线DC，点P为⊙O优弧AC上不与A、C重合的一个动点，点P从点C出发以每秒π个单位的速度顺时针匀速运动，到达点A停止运动．
    （1）求∠DCA的度数；
    （2）填空；
    ①当t=1s时，四边形OBPC是菱形；
    ②当t=3s时，由点A、P、C三点构成的三角形与△ABC全等．

    查看答案和解析>>

    同步练习册答案