
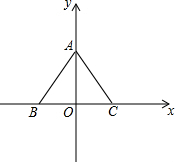
 如图,△ABC在平面直角坐标系中的位置如图所示,若S△ABC=12,BC=2OC,且AC,BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$.
如图,△ABC在平面直角坐标系中的位置如图所示,若S△ABC=12,BC=2OC,且AC,BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$.分析 (1)解方程组求出线段AC,BC的长;
(2)根据三角形的面积公式求出OA,设点E的坐标为(x,0),根据三角形的面积公式计算即可;
(3)分AC=AP、CA=CP,PA=CP三种情况,根据等腰三角形的性质计算即可.
解答 解:(1)$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$,
解方程组得,BC=6,AC=5;
(2)∵S△ABC=12,BC=6,
∴AO=4,
设点E的坐标为(x,0),
由题意得,$\frac{1}{2}×$|x|×4=$\frac{16}{3}$,
则|x|=$\frac{8}{3}$,
解得,x=±$\frac{8}{3}$,
∴点E的坐标为($\frac{8}{3}$,0)或(-$\frac{8}{3}$,0);
(3)当AC=AP时,点P的坐标为(-3,0),
当CA=CP,点P在点C的左侧时,CP=CA=5,
∴点P的坐标为(-1,0),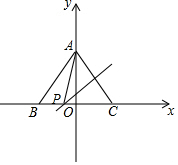
点P在点C的右侧时,CP=CA=5,
∴点P的坐标为(8,0),
当PA=PC时,如图,设OP=x,则PC=x+3,
则x2+42=(x+3)2,
解得,x=$\frac{7}{6}$,
∴点P的坐标为(-$\frac{7}{6}$,0),
∴点P的坐标为(-3,0)或(-1,0)或(8,0)或(-$\frac{7}{6}$,0)时,△ACP是以AC为腰的等腰三角形.
点评 本题考查的是等腰三角形的性质、三角形的面积计算,掌握等腰三角形的性质、灵活运用数形结合思想是解题的关键.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:填空题
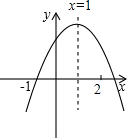 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有①③④.
已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有①③④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=3,BC=5.
如图,在四边形ABCD中,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=3,BC=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com