
”¾ĢāÄæ”æ×Ō2017Äź3ŌĀĘš£¬³É¶¼ŹŠÖŠŠÄ³ĒĒų¾ÓĆńÓĆĖ®ŹµŠŠŅŌ»§ĪŖµ„Ī»µÄČż¼¶½×ĢŻŹÕ·Ń°ģ·Ø£ŗ
µŚI¼¶£ŗ¾ÓĆńĆ滧ĆæŌĀÓĆĖ®18¶ÖŅŌÄŚŗ¬18¶ÖĆæ¶ÖŹÕĖ®·ŃaŌŖ£»
µŚ¢ņ¼¶£ŗ¾ÓĆńĆ滧ĆæŌĀÓĆĖ®³¬¹ż18¶Öµ«²»³¬¹ż25¶Ö£¬Ī“³¬¹ż18¶ÖµÄ²æ·Ö°“ÕÕµŚ¢ń¼¶±ź×¼ŹÕ·Ń£¬³¬¹ż²æ·ÖĆæ¶ÖŹÕĖ®·ŃbŌŖ£»
µŚ¢ó¼¶£ŗ¾ÓĆńĆ滧ĆæŌĀÓĆĖ®³¬¹ż25¶Ö£¬Ī“³¬¹ż25¶ÖµÄ²æ·Ö°“ÕÕµŚI”¢¢ņ¼¶±ź×¼ŹÕ·Ń£¬³¬¹ż²æ·ÖĆæ¶ÖŹÕĖ®·ŃcŌŖ£®
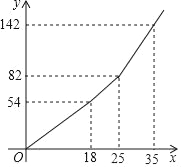
ÉčŅ»»§¾ÓĆńŌĀÓĆĖ®x¶Ö£¬Ó¦½ÉĖ®·ŃĪŖyŌŖ£¬yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾
£Ø1£©øł¾ŻĶ¼ĻóÖ±½Ó×÷“š£ŗa£½”” ””£¬b£½”” ””£»
£Ø2£©Ēóµ±x”Ż25Ź±yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£»
£Ø3£©°ŃÉĻŹöĖ®·Ń½×ĢŻŹÕ·Ń°ģ·Ø³ĘĪŖ·½°ø¢Ł£¬¼ŁÉč»¹“ęŌŚ·½°ø¢Ś£ŗ¾ÓĆńĆ滧ŌĀÓĆĖ®Ņ»ĀÉ°“ÕÕĆæ¶Ö4ŌŖµÄ±ź×¼½É·Ń£¬ĒėÄćøł¾Ż¾ÓĆńĆ滧ŌĀ”°ÓĆĖ®ĮæµÄ“óŠ”Éč¼Ę³ö¶Ō¾ÓĆń½É·Ń×īŹµ»ŻµÄ·½°ø£®£ØŠ“³ö¹ż³Ģ£©
”¾“š°ø”æ£Ø1£©3£»4£»£Ø2£©µ±x”Ż25Ź±£¬yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖy£½6x©68£»£Ø3£©µ±x£¼34Ź±£¬Ń”Ōń½É·Ń·½°ø¢ŁøüŹµ»Ż£»µ±x£½34Ź±£¬Ń”ŌńĮ½ÖÖ½É·Ń·½°ø·ŃÓĆĻąĶ¬£»µ±x£¾34Ź±£¬Ń”Ōń½É·Ń·½°ø¢ŚøüŹµ»Ż
”¾½āĪö”æ
£Ø1£©øł¾Żµ„¼Ū£½×ܼŪ”ĀŹżĮææÉĒó³öa£¬bµÄÖµ£¬“ĖĪŹµĆ½ā£»
£Ø2£©¹Ū²ģŗÆŹżĶ¼Ļó£¬ÕŅ³öµćµÄ×ų±ź£¬ĄūÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒó³öµ±x”Ż25Ź±yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£»
£Ø3£©ÓÉ×ܼŪ£½µ„¼Ū”ĮŹżĮææÉÕŅ³öŃ”Ōń½É·Ń·½°ø¢ŚŠč½»Ė®·Ńy£ØŌŖ£©ÓėÓĆĖ®ŹżĮæx£Ø¶Ö£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬·Ö±šÕŅ³öµ±6x©68£¼4x£¬6x©68£½4x£¬6x©68£¾4xŹ±xµÄȔֵ·¶Ī§£ØxµÄÖµ£©£¬Ń”Ōń·ŃÓƵĶµÄ·½°ø¼“æÉµĆ³ö½įĀŪ£®
£Ø1£©a£½54”Ā18£½3£¬
b£½£Ø82©54£©”Ā£Ø25©18£©£½4£®
¹Ź“š°øĪŖ£ŗ3£»4£®
£Ø2£©Éčµ±x”Ż25Ź±£¬yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖy£½mx+n£Øm”Ł0£©£¬
½«£Ø25£¬82£©£¬£Ø35£¬142£©“śČėy£½mx+n£¬µĆ£ŗ![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
”ąµ±x”Ż25Ź±£¬yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖy£½6x©68£®
£Ø3£©øł¾ŻĢāŅāµĆ£ŗŃ”Ōń½É·Ń·½°ø¢ŚŠč½»Ė®·Ńy£ØŌŖ£©ÓėÓĆĖ®ŹżĮæx£Ø¶Ö£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖy£½4x£®
µ±6x©68£¼4xŹ±£¬x£¼34£»
µ±6x©68£½4xŹ±£¬x£½34£»
µ±6x©68£¾4xŹ±£¬x£¾34£®
”ąµ±x£¼34Ź±£¬Ń”Ōń½É·Ń·½°ø¢ŁøüŹµ»Ż£»µ±x£½34Ź±£¬Ń”ŌńĮ½ÖÖ½É·Ń·½°ø·ŃÓĆĻąĶ¬£»µ±x£¾34Ź±£¬Ń”Ōń½É·Ń·½°ø¢ŚøüŹµ»Ż£®


 ĆūŠ£ĮŖĆĖæģĄÖæĪĢĆĻµĮŠ“š°ø
ĆūŠ£ĮŖĆĖæģĄÖæĪĢĆĻµĮŠ“š°ø »ĘøŌ““ÓžķĻµĮŠ“š°ø
»ĘøŌ““ÓžķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ØŅå£ŗČē¹ūŅ»ŌŖ¶ž“Ī·½³Ģ![]() Āś×ća+b+c=0£¬ĪŅĆĒ³ĘÕāøö·½³ĢĪŖ”°·ļ»Ė”±·½³Ģ£®ŅŃÖŖ
Āś×ća+b+c=0£¬ĪŅĆĒ³ĘÕāøö·½³ĢĪŖ”°·ļ»Ė”±·½³Ģ£®ŅŃÖŖ![]() ŹĒ·ļ»Ė·½³Ģ£¬ĒŅÓŠĮ½øöĻąµČµÄŹµŹżøł£¬ŌņĻĀĮŠÕżČ·µÄŹĒ£Ø””””£©
ŹĒ·ļ»Ė·½³Ģ£¬ĒŅÓŠĮ½øöĻąµČµÄŹµŹżøł£¬ŌņĻĀĮŠÕżČ·µÄŹĒ£Ø””””£©
A.a=cB.a=bC.b=cD.a=b=c
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬¶ž“ĪŗÆŹży£½ax2©2ax©3a£Øa£¼0£©µÄĶ¼ĻóÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄÓŅ²ą£©£¬ÓėyÖįµÄÕż°ėÖį½»ÓŚµćC£¬¶„µćĪŖD£®
£Ø1£©Ē󶄵ćDµÄ×ų±ź£ØÓĆŗ¬aµÄ“śŹżŹ½±ķŹ¾£©£»
£Ø2£©ČōŅŌADĪŖÖ±¾¶µÄŌ²¾¹żµćC£®
¢ŁĒóÅ×ĪļĻßµÄŗÆŹż¹ŲĻµŹ½£»
¢ŚČēĶ¼2£¬µćEŹĒyÖįøŗ°ėÖįÉĻŅ»µć£¬Į¬½ÓBE£¬½«”÷OBEČĘĘ½ĆęÄŚÄ³Ņ»µćŠż×Ŗ180”ć£¬µĆµ½”÷PMN£ØµćP”¢M”¢N·Ö±šŗĶµćO”¢B”¢E¶ŌÓ¦£©£¬²¢ĒŅµćM”¢N¶¼ŌŚÅ×ĪļĻßÉĻ£¬×÷MF”ĶxÖįÓŚµćF£¬ČōĻ߶ĪMF£ŗBF£½1£ŗ2£¬ĒóµćM”¢NµÄ×ų±ź£»
¢ŪµćQŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻ£¬ŅŌQĪŖŌ²ŠÄµÄŌ²¹żA”¢BĮ½µć£¬²¢ĒŅŗĶÖ±ĻßCDĻąĒŠ£¬ČēĶ¼3£¬ĒóµćQµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē¹ūČż½ĒŠĪÓŠŅ»±ßÉĻµÄÖŠĻß³¤Ē”ŗƵČÓŚÕā±ßµÄ³¤£¬ÄĒĆ“³ĘÕāøöČż½ĒŠĪĪŖŗĆĶęČż½ĒŠĪ£®ČōRt”÷ABCŹĒŗĆĶęČż½ĒŠĪ£¬ĒŅ”ĻC£½90”ć£¬BC”ŻAC£¬ŌņsinB£½_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬E£¬FĪŖ¶Ō½ĒĻßBDÉĻµÄĮ½µć£¬ĒŅ”ĻDAE£½”ĻBCF£®
ĒóÖ¤£ŗ£Ø1£©AE£½CF£»
£Ø2£©ĖıߊĪAECFŹĒĘ½ŠŠĖıߊĪ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬”ŃO¹żÕż·½ŠĪABCDµÄ¶„µćA”¢DĒŅÓė±ßBCĻąĒŠÓŚµćE£¬·Ö±š½»AB”¢DCÓŚµćM”¢N.¶ÆµćPŌŚ”ŃO»ņÕż·½ŠĪABCDµÄ±ßÉĻŅŌĆæĆėŅ»øöµ„Ī»µÄĖŁ¶Č×öĮ¬ŠųŌČĖŁŌĖ¶Æ.ÉčŌĖ¶ÆµÄŹ±¼äĪŖx£¬Ō²ŠÄOÓėPµćµÄ¾ąĄėĪŖy£¬Ķ¼2¼ĒĀ¼ĮĖŅ»¶ĪŹ±¼äĄļyÓėxµÄŗÆŹż¹ŲĻµ£¬ŌŚÕā¶ĪŹ±¼äĄļPµćµÄŌĖ¶ÆĀ·¾¶ĪŖ£Ø £©
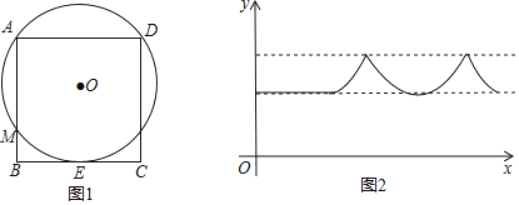
A. “ÓDµć³ö·¢£¬ŃŲ»”DA”ś»”AM”śĻ߶ĪBM”śĻ߶ĪBC
B. “ÓBµć³ö·¢£¬ŃŲĻ߶ĪBC”śĻ߶ĪCN”ś»”ND”ś»”DA
C. “ÓAµć³ö·¢£¬ŃŲ»”AM”śĻ߶ĪBM”śĻ߶ĪBC”śĻ߶ĪCN
D. “ÓCµć³ö·¢£¬ŃŲĻ߶ĪCN”ś»”ND”ś»”DA”śĻ߶ĪAB
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
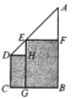
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬µć
£¬µć![]() ŹĒ±ß
ŹĒ±ß![]() ÉĻŅ»µć£¬¹żµć
ÉĻŅ»µć£¬¹żµć![]() ·Ö±š×÷
·Ö±š×÷![]() Óė
Óė![]() µÄ“¹Ļߣ¬¹żµć
µÄ“¹Ļߣ¬¹żµć![]() ×÷
×÷![]() µÄ“¹Ļߣ¬µĆµ½¾ŲŠĪ
µÄ“¹Ļߣ¬µĆµ½¾ŲŠĪ![]() ŗĶ¾ŲŠĪ
ŗĶ¾ŲŠĪ![]() £¬ŌņÕāĮ½øö¾ŲŠĪµÄĆ껿֮ŗĶµÄ×ī“óÖµŹĒ_________£®
£¬ŌņÕāĮ½øö¾ŲŠĪµÄĆ껿֮ŗĶµÄ×ī“óÖµŹĒ_________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
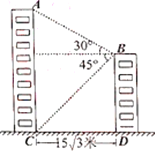
”¾ĢāÄæ”æČēĶ¼£¬Ä³Š£½ĢѧĀ„![]() ÓėŹµŃéĀ„
ÓėŹµŃéĀ„![]() µÄĖ®Ę½¼ä¾ą
µÄĖ®Ę½¼ä¾ą![]() Ć×£¬ŌŚŹµŃéĀ„¶„²æ
Ć×£¬ŌŚŹµŃéĀ„¶„²æ![]() µć²āµĆ½ĢѧĀ„¶„²æ
µć²āµĆ½ĢѧĀ„¶„²æ![]() µćµÄŃö½ĒŹĒ
µćµÄŃö½ĒŹĒ![]() £¬µ×²æ
£¬µ×²æ![]() µćµÄø©½ĒŹĒ
µćµÄø©½ĒŹĒ![]() £¬Ōņ½ĢѧĀ„
£¬Ōņ½ĢѧĀ„![]() µÄø߶ȏĒ____Ćףؽį¹ū±£ĮōøłŗÅ£©.
µÄø߶ȏĒ____Ćףؽį¹ū±£ĮōøłŗÅ£©.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±ĻßL£ŗy=©![]() x+2ÓėxÖį”¢yÖį·Ö±š½»ÓŚA”¢BĮ½µć£¬ŌŚyÖįÉĻÓŠŅ»µćN£Ø0£¬4£©£¬¶ÆµćM“ÓAµćŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŌČĖŁŃŲxÖįĻņ×óŅĘ¶Æ£®
x+2ÓėxÖį”¢yÖį·Ö±š½»ÓŚA”¢BĮ½µć£¬ŌŚyÖįÉĻÓŠŅ»µćN£Ø0£¬4£©£¬¶ÆµćM“ÓAµćŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŌČĖŁŃŲxÖįĻņ×óŅĘ¶Æ£®
£Ø1£©µćAµÄ×ų±ź£ŗ_____£»µćBµÄ×ų±ź£ŗ_____£»
£Ø2£©Ēó”÷NOMµÄĆ껿SÓėMµÄŅĘ¶ÆŹ±¼ätÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©ŌŚyÖįÓŅ±ß£¬µ±tĪŖŗĪÖµŹ±£¬”÷NOM”Õ”÷AOB£¬Ēó³ö“ĖŹ±µćMµÄ×ų±ź£»
£Ø4£©ŌŚ£Ø3£©µÄĢõ¼žĻĀ£¬ČōµćGŹĒĻ߶ĪONÉĻŅ»µć£¬Į¬½įMG£¬”÷MGNŃŲMGÕŪµž£¬µćNĒ”ŗĆĀäŌŚxÖįÉĻµÄµćH“¦£¬ĒóµćGµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com