
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,一个三角尺的直角顶点与
,一个三角尺的直角顶点与![]() 边的中点
边的中点![]() 重合,且两条直角边分别经过点
重合,且两条直角边分别经过点![]() 和点
和点![]() ,将三角尺绕点
,将三角尺绕点![]() 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与
按顺时针方向旋转任意一个锐角,当三角尺的两直角边与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() 时,下列结论中错误的是( )
时,下列结论中错误的是( )
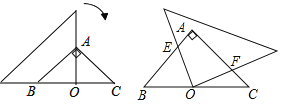
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】C
【解析】
连接AO,易证△EOA≌△FOC(ASA),利用全等三角形的性质可得出EA=FC,进而可得出AE+AF=AC,选项A正确;由三角形内角和定理结合∠B+∠C=90°,∠EOB+∠FOC=90°可得出∠BEO+∠OFC=180°,选项B正确;由△EOA≌△FOC可得出S△EOA=S△FOC,结合图形可得出S四边形AEOF=S△EOA+S△AOF=S△FOC+S△AOF=S△AOC=![]() S△ABC,选项D正确.综上,此题得解.
S△ABC,选项D正确.综上,此题得解.
连接AO,如图所示.
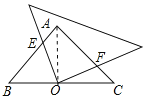
∵△ABC为等腰直角三角形,点O为BC的中点,
∴OA=OC,∠AOC=90°,∠BAO=∠ACO=45°.
∵∠EOA+∠AOF=∠EOF=90°,∠AOF+∠FOC=∠AOC=90°,
∴∠EOA=∠FOC.
在△EOA和△FOC中,
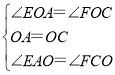 ,
,
∴△EOA≌△FOC(ASA),
∴EA=FC,
∴AE+AF=AF+FC=AC,选项A正确;
∵∠B+∠BEO+∠EOB=∠FOC+∠C+∠OFC=180°,∠B+∠C=90°,∠EOB+∠FOC=180°-∠EOF=90°,
∴∠BEO+∠OFC=180°,选项B正确;
∵△EOA≌△FOC,
∴S△EOA=S△FOC,
∴S四边形AEOF=S△EOA+S△AOF=S△FOC+S△AOF=S△AOC=![]() S△ABC,选项D正确.
S△ABC,选项D正确.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形![]() 中,点
中,点![]() 为对角线
为对角线![]() 上一动点(点
上一动点(点![]() 与点
与点![]() 、
、![]() 不重合),连接
不重合),连接![]() ,作
,作![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() 、
、![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]()
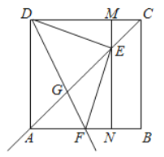
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
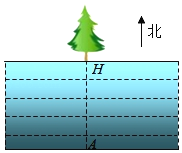
【题目】为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向.测量方案与数据如下表:
课题 | 测量河流宽度 | ||
测量工具 | 测量角度的仪器,皮尺等 | ||
测量小组 | 第一小组 | 第二小组 | 第三小组 |
测量方案示意图 |
|
|
|
说明 | 点B,C在点A的正东方向 | 点B,D在点A的正东方向 | 点B在点A的正东方向,点C在点A的正西方向. |
测量数据 | BC=60m, ∠ABH=70°, ∠ACH=35°. | BD=20m, ∠ABH=70°, ∠BCD=35°. | BC=101m, ∠ABH=70°, ∠ACH=35°. |
(1)哪个小组的数据无法计算出河宽?
(2)请选择其中一个方案及其数据求出河宽(精确到0.1m).(参考数据:sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
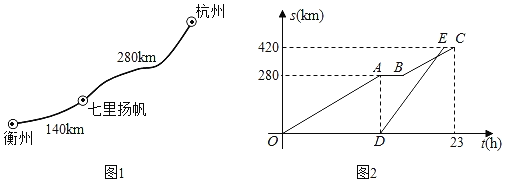
【题目】2020年5月16日,“钱塘江诗路”航道全线开通,一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h,游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变).
(1)写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.
(2)若货轮比游轮早36分钟到达衢州.问:
①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?
查看答案和解析>>
科目:初中数学 来源: 题型:
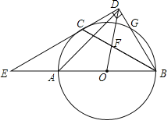
【题目】如图,AB为⊙O的直径,C,G是⊙O上两点,且弧AC=弧CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校举行“经典诵读”比赛,诵读材料有:A《唐诗》、B《宋词》、C《论语》.将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小红和小亮参加诵读比赛,比赛时小红先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行比赛.
(1)小红诵读《论语》的概率是 ;
(2)请用列表法或画树状图的方法,求小红和小亮诵读两个相同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组建了书法、音乐、美术、舞蹈、演讲5个社团,随机调查了部分学生.被调查学生每人都参加且只参加了其中一个社团活动,并将调查结果制成了如图两幅不完整的统计图,在扇形统计图中,“音乐”所对应的扇形圆心角度数是( )度.
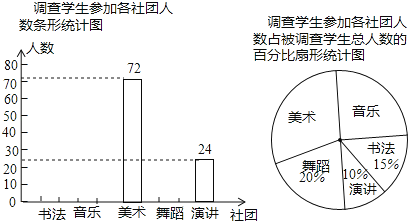
A.25%B.25C.60D.90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的四个顶点坐标分别是
的四个顶点坐标分别是![]() 、
、![]() 、
、![]() 、
、![]() .函数
.函数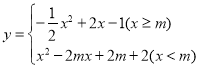 (
(![]() 为常数).
为常数).
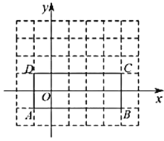
(1)当此函数的图象经过点![]() 时,求此函数的表达式;
时,求此函数的表达式;
(2)在(1)的条件下,当![]() 时,求函数值
时,求函数值![]() 的取范围;
的取范围;
(3)当此函数的图象与矩形![]() 的边有两个交点时,直接出
的边有两个交点时,直接出![]() 的取值范围;
的取值范围;
(4)记此函数在![]() 范围内的纵坐标为
范围内的纵坐标为![]() ,若存在
,若存在![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com