
【题目】如图,AB∥CD,OA=OD,点F、D、O、A、E在同一直线上,AE=DF,求证:EB∥CF.

【答案】证明见解析
【解析】试题分析:由AB与CD平行,利用两直线平行得到两对内错角相等,再由OA=OD,利用AAS得到△AOB≌△DOC,利用全等三角形对应边相等得到OC=OB,由OA+AE=OD+DF求出OF=OE,夹角为对顶角相等,利用SAS得到△COF≌△BOE,利用全等三角形对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
试题解析:∵AB∥CD, ∴∠DCO=∠ABO,∠CDO=∠BAO, 在△AOB和△DOC中,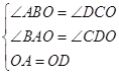 , ∴△AOB≌△DOC(AAS), ∴OC=OB, ∵OA=OD,AE=DF, ∴OA+AE=OD+DF,即OE=OF, 在△COF和△BOE中,
, ∴△AOB≌△DOC(AAS), ∴OC=OB, ∵OA=OD,AE=DF, ∴OA+AE=OD+DF,即OE=OF, 在△COF和△BOE中, , ∴△COF≌△BOE(SAS), ∴∠F=∠E, ∴BE∥CF.
, ∴△COF≌△BOE(SAS), ∴∠F=∠E, ∴BE∥CF.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,

(1)求证:DB=DE.
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )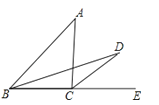
A.46°
B.92°
C.44°
D.23°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个三角形的纸片ABC,其中∠A=∠C.
(1)把△ABC纸片按(如图1)所示折叠,使点A落在BC边上的点F处,DE是折痕,说明BC∥DF;
(2)把△ABC纸片沿DE折叠,当点A落在四边形BCED内时 (如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;
(3)当点A落在四边形BCED外时(如图3),∠C与∠1、∠2的关系是(直接写出结论)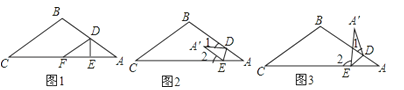
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行射击10次,它们的平均成绩均为7环,10次射击成绩的方差分别是:S2甲=3,S2乙=1.2.成绩较为稳定的是______.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国科学家屠呦呦获得2015年诺贝尔生理学或医学奖,她研发的抗疟新药每年为110万婴幼儿免除了疟疾的危害.其中110万用科学记数法表示为( )
A.11×103
B.1.1×104
C.1.1×106
D.1.1×108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com