
【题目】如图1是一个新款水杯,水杯不盛水时按如图2所示的位置放置,这样可以快速晾干杯底,干净透气;将图2的主体部分的抽象成图3,此时杯口与水平直线的夹角35°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F. 
(1)求∠BAF的度数;(sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
(2)求点A到水平直线CE的距离AF的长(精确到0.1cm)
【答案】
(1)解:作BM⊥AF于M,BN⊥CF于N.
∵AF⊥EN,
∴∠MFN=∠BMF=∠BNF=90°,
∴四边形BMFN是矩形.
∴BM∥FN,
∴∠MBC=∠BCN=35°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABM=90°﹣∠MBC=55°,
∴∠FAB=90°﹣∠ABM=35°,
故答案为35°
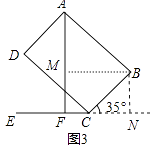
(2)解:在Rt△CBN中,∵BC=8,
∴FM=NB=BCtan35°=0.5736×8≈4.59,
在Rt△ABM中,AM=ABcos35°=10×0.8102≈8.20,
∴AF=AM+FM=8.20+4.59≈12.8(cm)
【解析】(1)作BM⊥AF于M,BN⊥CF于N.由BM∥FN,推出∠MBC=∠BCN=35°,由题意∠ABM=90°﹣∠MBC=55°,推出∠FAB=90°﹣∠ABM=35°.(2)分别在Rt△CBN,Rt△ABM中求出AM、BN即可解决问题.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。
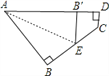
(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E,F分别是边BC,CD边上的动点,且AE=AF,设△AEF的面积为y,EC的长为x.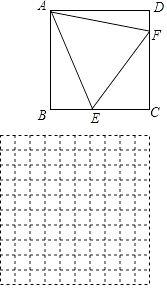
(1)求y与x之间的函数表达式,并写出自变量x的取值范围.
(2)当x取何值时,△AEF的面积最大,最大面积是多少?
(3)在直角坐标系中画出y关于x的函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(1)如图(1),等边△ABC内有一点P到顶点A,B,C的距离分别为3,4,5,则∠APB= .
分析:由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌ , 这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(2)请你利用第(1)题的解答思想方法,解答下面问题:已知如图(2),△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:BE2+CF2=EF2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
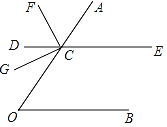
【题目】已知:点C在∠AOB的一边OA上,过点C的直线DE∥O B.做∠ACD的平分线CF,过点C画CF的垂线CG,如图所示.
(Ⅰ)若∠AOB=40°,求∠ACD及∠ECF的度数;
(Ⅱ)求证:CG平分∠OCD;
(Ⅲ)延长FC交OB于点H,用直尺和三角板过点O作OR⊥FH,垂足为R,过点O
作FH的平行线交ED于点Q.先补全图形,再证明∠COR=∠GCO,∠CQO=∠CHO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若菱形![]() 的边长为2,
的边长为2, ![]() .求
.求![]() 的长.
的长.
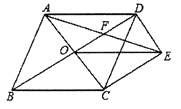
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,可得OE=CD即可;
(2)根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
(1)证明:在菱形ABCD中,OC=![]() AC.
AC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD=![]() .
.
在Rt△ACE中,
AE=![]() .
.
点睛:本题考查了菱形的性质,矩形的判定与性质,勾股定理的应用,是基础题,熟记矩形的判定方法与菱形的性质是解题的关键.
【题型】解答题
【结束】
25
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
(1)求反比例函数与一次函数的表达式;
(2)结合图像写出不等式![]() 的解集;
的解集;
(3)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投掷一枚质地均匀的正方体骰子.
(1)下列说法中正确的有 . (填序号)
①向上一面点数为1点和3点的可能性一样大;
②投掷6次,向上一面点数为1点的一定会出现1次;
③连续投掷2次,向上一面的点数之和不可能等于13.
(2)如果小明连续投掷了10次,其中有3次出现向上一面点数为6点,这时小明说:投掷正方体骰子,向上一面点数为6点的概率是![]() . 你同意他的说法吗?说说你的理由.
. 你同意他的说法吗?说说你的理由.
(3)为了估计投掷正方体骰子出现6点朝上的概率,小亮采用转盘来代替骰子做实验.下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上红、白两种颜色,使得转动转盘,当转盘停止转动后,指针落在红色区域的概率与投掷正方体骰子出现6点朝上的概率相同.(友情提醒:在转盘上用文字注明颜色和扇形圆心角的度数.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com