
分析 (1)设熟练工和新工人每月分别可以安装x辆和y辆汽车,根据题意列出方程组,解出方程组即是所求;
(2)设熟练工人数为m,根据题意列出方程,分析m取各值时,n的数值是多少;
(3)由熟练工的工作量是新员工的2倍,而工资不到2倍,可知熟练工在满足要求的情况下越多越好.
解答 解:(1)设每名熟练工和新工人每月分别可以安装x辆和y辆汽车,
根据题意得:$\left\{\begin{array}{l}{x+2y=8}\\{2x+3y=14}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,
则每名熟练工和新工人每月分别可以安装4辆和2辆汽车.
(2)设熟练工数为m名,则新工人数为mn,
根据题意得:(2mn+4m)×12=240,
当m=1时,n=8;
当m=2时,n=3;
当m=3时,n=$\frac{4}{3}$;
当m=4时,n=$\frac{1}{2}$;
当m=5时,n=0(舍去).
故工厂有四种招聘方案,分别为:1名熟练工招8名新工人,2名熟练工每人招3名新工人,3名熟练工每人招$\frac{4}{3}$名新工人,4名熟练工每人招$\frac{1}{2}$名新工人.
(3)由(2)得知4种生产方式,1名熟练工和8名新工人;2名熟练工和6名新工人;3名熟练工和4名新工人,4名熟练工和2名新工人,
因为新工人的数量多余熟练工,所以只有前三种方案可供选择,
方案一:W=1×2000+8×1200=11600(元);
方案二:W=2×2000+6×1200=11200(元);
方案三:W=3×2000+4×1200=10800(元),
故工厂应招聘4名新工人,这样每月支出的金额最少.
点评 本题考查了一次函数的应用,解题的关键是根据题意列出正确的方程,并能熟练的利用各种方法解方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
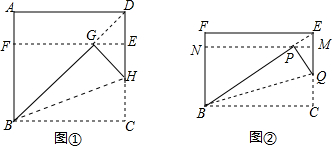 定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.
定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在梯形ABCD中,AD∥BC,∠B=45°,点E是AB的中点,DE=DC,∠EDC=90°,若AB=2,则AD的长是$\frac{\sqrt{2}}{2}$.
如图,在梯形ABCD中,AD∥BC,∠B=45°,点E是AB的中点,DE=DC,∠EDC=90°,若AB=2,则AD的长是$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
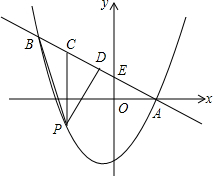 如图,直线y=-$\frac{1}{2}$x+1与y轴交于点E,与抛物线y=ax2-bx-3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线A,B下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
如图,直线y=-$\frac{1}{2}$x+1与y轴交于点E,与抛物线y=ax2-bx-3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线A,B下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com