

分析 (1)根据频数之和等于总数求得40~50的频数即可补全图形;
(2)先根据百分比之和为1求得C的百分比,再乘以360°可得;
(3)将垃圾总量乘以可回收垃圾所占百分比即可得.
解答 解:(1)由条形图可知40~50的频数为100-(5+15+40+10)=30,如图所示,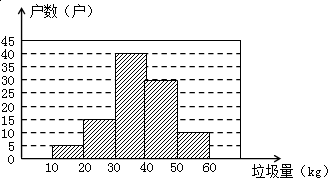
(2)“有害垃圾C”所占的百分比为1-(48%+32%+17%)=3%,
∴表示“有害垃圾C”所在扇形的圆心角度数为360°×3%=10.8°,
故答案为:10.8;
(3)∵2750×48%=1320(kg),
∴可回收的垃圾约为1320kg,
故答案为:1320.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小,掌握频数之和等于总数、百分比之和为1是解题的关键.


科目:初中数学 来源: 题型:解答题
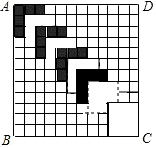 如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.请你认真观察思考后回答下列问题:
如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.请你认真观察思考后回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
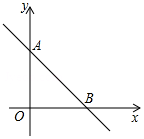 如图,直线y=$\frac{\sqrt{3}}{3}x$+1和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是($\sqrt{3}$,2)或(0,-1).
如图,直线y=$\frac{\sqrt{3}}{3}x$+1和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是($\sqrt{3}$,2)或(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠BAC=45°,过A、B两点的⊙O交AC于点D,且OD∥BC,OD交AB于点E.
如图,△ABC中,∠BAC=45°,过A、B两点的⊙O交AC于点D,且OD∥BC,OD交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为1.
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
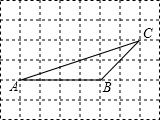 如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)
如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在线段BF上,有点E、C,BE=CF,∠B=∠F,∠ACB=∠DEF.
如图,在线段BF上,有点E、C,BE=CF,∠B=∠F,∠ACB=∠DEF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com