
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),将该抛物线位于
的左侧),将该抛物线位于![]() 轴上方曲线记作
轴上方曲线记作![]() ,将该抛物线位于
,将该抛物线位于![]() 轴下方部分沿
轴下方部分沿![]() 轴翻折,翻折后所得曲线记作
轴翻折,翻折后所得曲线记作![]() ,曲线
,曲线![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求曲线![]() 所在抛物线相应的函数表达式;
所在抛物线相应的函数表达式;
(2)求![]() 外接圆的半径;
外接圆的半径;
(3)点![]() 为曲线
为曲线![]() 或曲线
或曲线![]() 上的一个动点,点
上的一个动点,点![]() 为
为![]() 轴上的一个动点,若以点
轴上的一个动点,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)
;(2) ![]() ;(3)点
;(3)点![]() 的坐标分别为
的坐标分别为![]()
![]() .
.
【解析】
试题分析:(1) 把![]() 化为顶点式,求得该抛物线的顶点坐标和开口方向,由翻折可得曲线
化为顶点式,求得该抛物线的顶点坐标和开口方向,由翻折可得曲线![]() 所在抛物线的顶点坐标和开口方向,即可得曲线
所在抛物线的顶点坐标和开口方向,即可得曲线![]() 的解析式;(2)先求得
的解析式;(2)先求得![]() 外接圆圆心的坐标,再利用勾股定理求得半径的长即可;(3)分点P位于曲线M上和点P位于曲线N上两种情况求点Q的坐标即可.
外接圆圆心的坐标,再利用勾股定理求得半径的长即可;(3)分点P位于曲线M上和点P位于曲线N上两种情况求点Q的坐标即可.
试题解析:(1)因为![]() 可化为
可化为![]() ,
,
所以抛物线![]() 的点的坐标为(1,-4),开口向上,
的点的坐标为(1,-4),开口向上,
所以曲线![]() 所在抛物线的顶点坐标为(1,4),开口向下,
所在抛物线的顶点坐标为(1,4),开口向下,
故曲线![]() 所在抛物线相应的函数表达式为
所在抛物线相应的函数表达式为![]() ,
,
即![]() ;
;
(2)因为抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,
两点,
所以A(-1,0),B(3,0),则线段AB的垂直平分线的直线为x=1,
因为曲线![]() 交
交![]() 轴于点(0,3),
轴于点(0,3),
所以OC=OB,又∠COB=90°,所以线段BC的垂直平分线为直线y=x,
联立![]() ,解得
,解得![]() ,所以△ABC的外接圆圆心坐标为(1,1),
,所以△ABC的外接圆圆心坐标为(1,1),
由勾股定理可得![]() ,所以△ABC的外接圆半径为
,所以△ABC的外接圆半径为![]() ;
;
(3)过点C作直线l∥x轴,交曲线M或N于点P,
①当点P位于曲线M上时,
由![]() ,解得
,解得![]() ,
,
所以CP=![]() ,H或CP=
,H或CP=![]() ;
;
因为以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
所以CP∥BQ且CP=BQ,
所以![]() ;
;
②当点P位于曲线N上时,
由![]() ,解得
,解得![]() (舍去),
(舍去),
所以CP=2;
因为以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
所以CP∥BQ且CP=BQ,
所以![]() ;
;
综上所述,点![]() 的坐标分别为
的坐标分别为![]()
![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .点
.点![]() 在函数图像上,
在函数图像上,![]() 轴,且
轴,且![]() ,直线
,直线![]() 是抛物线的对称轴,
是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求![]() 、
、![]() 的值;
的值;
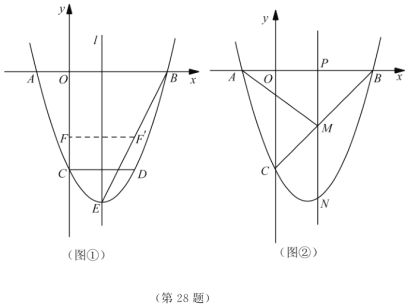
(2)如图①,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)如图②,动点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线分别与
轴的垂线分别与![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等,且线段
的面积相等,且线段![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:
时间 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
新加入人数(人) | 153 | 550 | 653 | b | 725 |
累计总人数(人) | 3353 | 3903 | a | 5156 | 5881 |
(1)表格中a= ,b= ;
(2)请把下面的条形统计图补充完整;
(3)根据以上信息,下列说法正确的是 (只要填写正确说法前的序号).
①在活动之前,该网站已有3200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2528人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和哥哥在环形跑道上练习长跑.他们从同一起点沿相反方向同时出发,每隔25秒钟相遇一次.现在,他们从同一起跑点沿相同方向同时出发,经过25分钟哥哥追上了小明,并且比小明多跑了20圈,求:
(1)哥哥速度是小明速度的多少倍?
(2)哥哥追上小明时,小明跑了多少圈?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期浙江大学的科学家们研制出今为止世界上最轻的材料,这种被称为“全碳气凝胶”的固态材料密度仅每立方厘米0.00016克,数据0.00016用科学记数法表示应是( )
A.1.6×104
B.0.16×10﹣3
C.1.6×10﹣4
D.16×10﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
(1)【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
已知:如图,
在 ![]() △
△![]() 中,
中, ![]() °,
°, ![]() °.
°.
求证: ![]() .
.
(2)【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得 ![]() ,
, ![]() ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度 ![]() .
.
求:桌面与地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com