
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,CD,由以BC为直径的⊙O,可得CD⊥AB,又由等腰三角形ABC的底角为30°,可得AD=BD,即可证得OD∥AC,继而可证得结论;
(2)首先根据三角函数的性质,求得BD,DE,AE的长,然后求得△BOD,△ODE,△ADE以及△ABC的面积,继而求得答案.
试题解析:(1)证明:连接OD,CD,
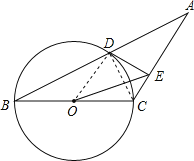
∵BC为⊙O直径,
∴∠BDC=90°,
即CD⊥AB,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵D点在⊙O上,
∴DE为⊙O的切线;
(2)解:∵∠A=∠B=30°,BC=4,
∴CD=![]() BC=2,BD=BCcos30°=2
BC=2,BD=BCcos30°=2![]() ,
,
∴AD=BD=2![]() ,AB=2BD=4
,AB=2BD=4![]() ,
,
∴S△ABC=![]() ABCD=
ABCD=![]() ×4
×4![]() ×2=4
×2=4![]() ,
,
∵DE⊥AC,
∴DE=![]() AD=
AD=![]() ×2
×2![]() =
=![]() ,
,
AE=ADcos30°=3,
∴S△ODE=![]() ODDE=
ODDE=![]() ×2×
×2×![]() =
=![]() ,
,
S△ADE=![]() AEDE=
AEDE=![]() ×
×![]() ×3=
×3=![]() ,
,
∵S△BOD=![]() S△BCD=
S△BCD=![]() ×
×![]() S△ABC=
S△ABC=![]() ×4
×4![]() =
=![]() ,
,
∴S△OEC=S△ABC-S△BOD-S△ODE-S△ADE=4![]() -
-![]() -
-![]() -
-![]() =
=![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】小强的钱包内有10元钱、20元钱和50元钱的纸币各1张.
(1)若从中随机取出1张纸币,求取出纸币的金额是20元的概率;
(2)若从中随机取出2张纸币,求取出纸币的总额可购买一件51元的商品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
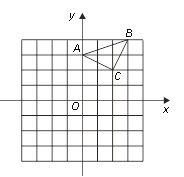
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】个体户王某经营一家饭馆,下面是饭馆所有工作人员在某个月份的工资;王某3000元,厨师甲450元,厨师乙400元,杂工320元,招待甲350元,招待乙320元,会计410元.
![]() 计算工作人员的平均工资;
计算工作人员的平均工资;
![]() 计算出的平均工作能否反映帮工人员这个月收入的一般水平?
计算出的平均工作能否反映帮工人员这个月收入的一般水平?
![]() 去掉王某的工资后,再计算平均工资;
去掉王某的工资后,再计算平均工资;
![]() 后一个平均工资能代表一般帮工人员的收入吗?
后一个平均工资能代表一般帮工人员的收入吗?
![]() 根据以上计算,从统计的观点看,你对
根据以上计算,从统计的观点看,你对![]() 的结果有什么看法?
的结果有什么看法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年6月11日,神舟十号飞船发射成功,神舟十号飞船身高9米,重约8吨,飞行速度约每秒7900米,将数7900用科学记数法表示,表示正确的是( )
A.0.79×104
B.7.9×104
C.7.9×103
D.0.79×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在﹣2,﹣3,4这三个数中任选2个数分别作为点P的横坐标和纵坐标.
(1)可得到的点得个数为 ;
(2)求过P点的正比例函数图象经过第二,四象限的概率(用树形图或列表法求解);
(3)过点P得正比例函数中,函数y随自变量x的增大而增大的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
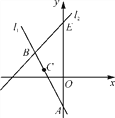
【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com