
【题目】如图,在平面直角坐标系xOy中,直线BC与抛物线y=x2+bx+c交于点B(3,0)和点C(0,3),抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积.
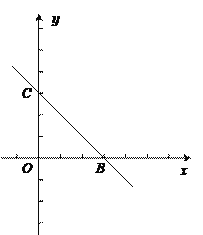
【答案】(1)y=x2﹣4x+3(2)3
【解析】分析:(1)、利用待定系数法求出一次函数和抛物线的函数解析式;(2)、过点C作CE∥x轴,过点B作EF∥y轴,过点D作DF∥x轴,根据S△DBC=S四边形CEFG﹣S△CDG﹣S△BFD﹣S△BCE得出答案.
详解:(1)设直线BC的解析式y=kx+b(k≠0),将点B(3,0)C(0,3)代入得:
![]() 解得
解得![]() , ∴直线BC的解析式为y=﹣x+3.
, ∴直线BC的解析式为y=﹣x+3.
将B(3,0),C(0,3)代入抛物线的解析式得:![]() , 解得:b=﹣4,c=3,
, 解得:b=﹣4,c=3,
∴抛物线的解析式为y=x2﹣4x+3.
(2)如图1所示:过点C作CE∥x轴,过点B作EF∥y轴,过点D作DF∥x轴.
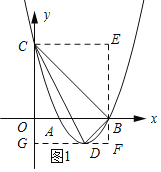
y=x2﹣4x+3=(x﹣2)2﹣1. ∴D(2,﹣1).
∴S△DBC=S四边形CEFG﹣S△CDG﹣S△BFD﹣S△BCE=12﹣![]() ×2×4﹣
×2×4﹣![]() ×1×1﹣
×1×1﹣![]() ×3×3=3.
×3×3=3.


科目:初中数学 来源: 题型:
【题目】如图为一座抛物线型的拱桥,AB、CD分别表示两个不同位置的水面宽度,O为拱桥顶部,水面AB宽为10米,AB距桥顶O的高度为12.5米,水面上升2.5米到达警戒水位CD位置时,水面宽为( )米.

A. 5 B. 2![]() C. 4
C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
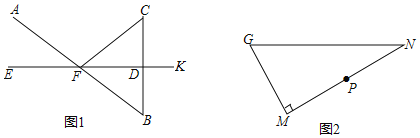
【题目】(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
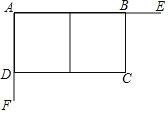
【题目】如图,某工程队在工地互相垂直的两面墙AE、AF处,用180米长的铁栅栏围成一个长方形场地ABCD,中间用同样材料分割成两个长方形.已知墙AE长120米,墙AF长40米,要使长方形ABCD的面积为4000平方米,问BC和CD各取多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
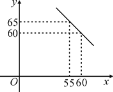
【题目】某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)试确定y与x之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
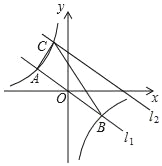
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).

A. 8cm B. 10cm C. 11cm D. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com