
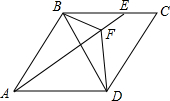
 如图,BD是菱形ABCD的对角线,点E是边BC上的动点,连接AE,点F在线段AE上,连接BF,DF,且∠AFB=60°,AB=BD
如图,BD是菱形ABCD的对角线,点E是边BC上的动点,连接AE,点F在线段AE上,连接BF,DF,且∠AFB=60°,AB=BD分析 (1)如图1过B作BH⊥AD于H,证得△ABD是等边三角形,得到∠BAD=60°,求出BH=3$\sqrt{3}$,即可得到结果;
(2)如图2,在AE上截取FG=BF,连接BG得到△BGF是等边三角形,求出BG=BF=GF,∠1+∠2=∠2+∠3=60°,得到∠1=∠3,推出△ABG≌△BDG,得到AG=BF,即可得到结论.
解答  解:(1)如图1,过B作BH⊥AD于H,
解:(1)如图1,过B作BH⊥AD于H,
∵四边形ABCD是菱形,
∴AB=AD,
∵AB=BD,
∴△ABD是等边三角形,
∴∠BAD=60°,
∴BH=3$\sqrt{3}$,
∴四边形ABCD的面积=AD•BH=6×$3\sqrt{3}$=18$\sqrt{3}$;
(2)如图2,在AE上截取FG=BF,连接BG,
∵∠AFB=60°,
∴△BGF是等边三角形,
∴BG=BF=GF,∠1+∠2=∠2+∠3=60°,
∴∠1=∠3,
在△ABG与△DFB中,
$\left\{\begin{array}{l}{BG=BF}\\{∠1=∠3}\\{AB=BD}\end{array}\right.$,
∴△ABG≌△BDG,
∴AG=BF,
∴AF=AG+GF,
即AF=DF+BF.
点评 本题考查了菱形的性质,求菱形的面积,全等三角形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
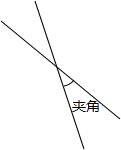 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
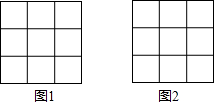 如图,在3×3的正方形网格中,每个小正方形的边长都是1,每个小格的顶点叫格点,以格点为顶点,分别按下列要求画三角形:
如图,在3×3的正方形网格中,每个小正方形的边长都是1,每个小格的顶点叫格点,以格点为顶点,分别按下列要求画三角形:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
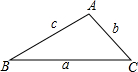 如图,△ABC中,∠BAC=120°,∠ABC=15°,∠A,∠B,∠C的对边分别是a,b,c,则a:b:c=2$\sqrt{3}$:($\sqrt{6}$-$\sqrt{2}$):2$\sqrt{2}$.
如图,△ABC中,∠BAC=120°,∠ABC=15°,∠A,∠B,∠C的对边分别是a,b,c,则a:b:c=2$\sqrt{3}$:($\sqrt{6}$-$\sqrt{2}$):2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com