解:(1)两个方程组各取一个方程重新组合得
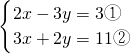
,
①×2+②×3得,13x=39,
解得x=3,
把x=3代入①得,6-3y=3,
解得y=1,
所以,方程组的解是

,
把方程组的解代入另两个方程得,
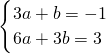
,
解得
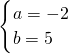
,
所以,ab=(-2)×5=-10;
(2)
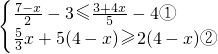
,
解不等式①,5(7-x)-30≤2(3+4x)-40,
35-5x-30≤6+8x-40,
-13x≤-39,
x≥3,
解不等式②,5x+60-15x≥24-6x,
5x-15x+6x≥24-60,
-4x≥-36,
x≤9,
所以不等式组的解集是3≤x≤9.
在数轴上表示如下:

分析:(1)先把两个方程组中的第一个方程联立组成新的方程组,求解得到x、y的值,再分别代入两个方程组的第二个方程得到关于a、b的二元一次方程组求解得到a、b的值,然后代入代数式进行计算即可得解;
(2)先求出两个不等式的解集,再求其公共解.
点评:本题考查了一元一次不等式组的解法,在数轴上表示不等式组的解集,需要把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示,(1)题解法先把只含有未知数x、y的方程重新组合成方程组求出x、y的值是解题的关键.

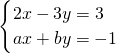 与
与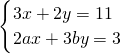 的解相同,求ab的值.
的解相同,求ab的值.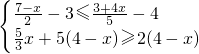 .
.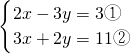 ,
, ,
,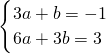 ,
,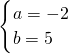 ,
,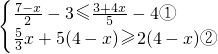 ,
,


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案