练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．先化简，再求值：（1+$\frac{1}{{x}^{2}-1}$）÷（x-$\frac{x}{x+1}$），其中x=$\sqrt{3}$+1．

    分析 原式括号中两项通分并利用同分母分式的加减法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．

    解答 解：原式=$\frac{{x}^{2}-1+1}{（x+1）（x-1）}$÷$\frac{{x}^{2}+x-x}{x+1}$=$\frac{{x}^{2}}{（x+1）（x-1）}$•$\frac{x+1}{{x}^{2}}$=$\frac{1}{x-1}$，
    当x=$\sqrt{3}$+1时，原式=$\frac{\sqrt{3}}{3}$．

    点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．若扇形的半径为3，扇形的面积为2π，则该扇形的圆心角为80度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知代数式-4xm+1y6与x2ny3m是同类项，则m=2，n=$\frac{3}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．若函数y=mx2+（m-1）x+$\frac{1}{2}$（m-1）的图象与x轴只有一个交点，那么m的值是（　　）
    A．0B．0，-1或1C．1或-1D．0或1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知正数a，b，c满足a+c=2b，求$\frac{1}{\sqrt{a}+\sqrt{b}}$+$\frac{1}{\sqrt{b}+\sqrt{c}}$-$\frac{2}{\sqrt{a}+\sqrt{c}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

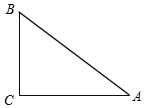    9．在Rt△ABC中，∠C=90°，AC=4，BC=3，
    （1）AB=5；
    （2）若经过点C且与边AB相切的动圆与边CB、CA分别相交于点E、F，则线段EF长度的取值范围是$\frac{12}{5}$≤EF＜4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．（1）已知m+n=8，mn=15，求m2-mn+n2的值．
    （2）已知a2+a-1=0，求a3+2a2+2016的值．
    （3）已知a+$\frac{1}{a}$=$\sqrt{7}$，求a-$\frac{1}{a}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

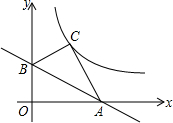    13．如图，已知点A（6，0），B（0，2$\sqrt{3}$），O为坐标原点，点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

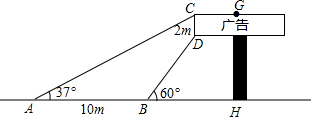    14．如图，长方形广告牌架在楼房顶部，已知CD=2m，经测量得到∠CAH=37°，∠DBH=60°，AB=10m，求GH的长．（参考数据：tan37°≈0.75，$\sqrt{3}$≈1.732，结果精确到0.1m）

    查看答案和解析>>

    同步练习册答案