
 如图,AB∥DC,且AD∥BC,∠α=50°,求∠C的度数.
如图,AB∥DC,且AD∥BC,∠α=50°,求∠C的度数. 科目:初中数学 来源: 题型:解答题
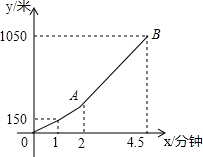 星期天的早晨,小明步行从家出发,到离家1050m的书店买书.出发1分钟后,他到达离家150m的地方,又过一分钟后,小明加快了速度.如图,是小明从家出发后,小明离家的路程y(米)与他行驶时间x(分钟)之间的函数图象.根据图象回答问题:
星期天的早晨,小明步行从家出发,到离家1050m的书店买书.出发1分钟后,他到达离家150m的地方,又过一分钟后,小明加快了速度.如图,是小明从家出发后,小明离家的路程y(米)与他行驶时间x(分钟)之间的函数图象.根据图象回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
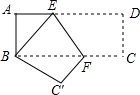 如图,长方形ABCD中,AD=8cm,AB=4cm,沿EF折叠,使点D落到点B处,点C落到点C′处
如图,长方形ABCD中,AD=8cm,AB=4cm,沿EF折叠,使点D落到点B处,点C落到点C′处查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com