
| A. | 2,0.4 | B. | 3,0.2 | C. | 3,0.4 | D. | 3,2 |
分析 根据平均数的定义先求出x的值,再众根据数的定义、以及方差公式进行计算即可得出答案.
解答 解:根据题意得,
2+x+4+3+3=3×5,
解得x=3,
则一组数据2,3,4,3,3的众数为3,
则这组数据的方差为$\frac{1}{5}$×[(2-3)2+3×(3-3)2+(4-3)2]=0.4.
故选:C.
点评 此题考查了众数、平均数和方差,用到的知识点是众数、平均数和方差,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2];众数是一组数据中出现次数最多的数.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
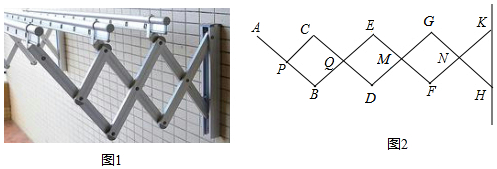
 如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
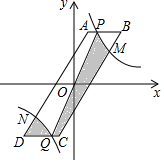 如图,在平面直角坐标系中,?ABCD的对称中心是原点O,点A、D的坐标分别为(1,3)、(-3,-3),动点P在边AB上,过点P的反比例函数y=$\frac{k}{x}$的图象交边CD于点Q,连接PQ.
如图,在平面直角坐标系中,?ABCD的对称中心是原点O,点A、D的坐标分别为(1,3)、(-3,-3),动点P在边AB上,过点P的反比例函数y=$\frac{k}{x}$的图象交边CD于点Q,连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2分 | B. | 4分 | C. | 6分 | D. | 8分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
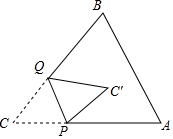 如图,△ABC,∠C=45°,点P、Q分别在射线CA、CB上,且CP=2,将△ABC沿PQ折叠,点C落在平面上点C′处.
如图,△ABC,∠C=45°,点P、Q分别在射线CA、CB上,且CP=2,将△ABC沿PQ折叠,点C落在平面上点C′处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com