
分析 分类讨论:当BE=BC时,如图1,利用sin∠AEB=$\frac{AB}{BE}$=$\frac{1}{2}$可得到∠AEB=30°;当CE=CB,如图2,同样方法可得∠CED=30°,再利用AD∥BC得到∠BCE=30°,∠CBE=∠AEB,接着根据等腰三角形的性质和三角形内角和得到∠CBE=75°,于是得到∠AEB=75°,综上所述,∠AEB的度数为30°或75°.
解答 解:当BE=BC时,如图1,
∵四边形ABCD为矩形,
∴BC=AD=2AB,∠A=90°,
∴BE=2AB,
在Rt△ABE中,∵sin∠AEB=$\frac{AB}{BE}$=$\frac{1}{2}$,
∴∠AEB=30°;
当CE=CB,如图2,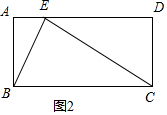
同样可得∠CED=30°,
∵AD∥BC,
∴∠BCE=30°,∠CBE=∠AEB,
∵CE=CB,
∴∠CBE=∠CEB,
∴∠CBE=$\frac{1}{2}$(180°-30°)=75°,
∴∠AEB=75°,
综上所述,∠AEB的度数为30°或75°.
故答案为30°或75°.
点评 本题考查了矩形的性质:平行四边形的性质矩形都具有;矩形的四个角都是直角.也考查了等腰三角形的性质.


科目:初中数学 来源: 题型:解答题
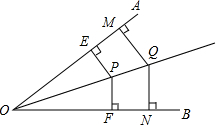 如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.
如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
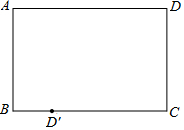 折纸:有一张矩形纸片ABCD(如图所示),要将点D沿某条直线翻折180°,恰好落在BC边上的点D′处,请在图中用尺规作出该直线.(保留作图痕迹)
折纸:有一张矩形纸片ABCD(如图所示),要将点D沿某条直线翻折180°,恰好落在BC边上的点D′处,请在图中用尺规作出该直线.(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
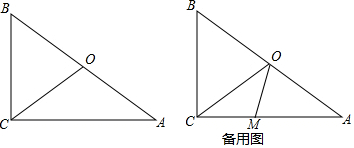
 在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com