
【题目】如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.
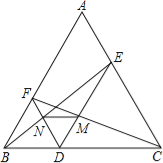
【答案】△DMN为等边三角形,理由见解析.
【解析】试题分析:由已知可得△BDF、△EDC是等边三角形,从而可证△BDE≌△FDC,继而可证△NDE≌△MDC,从而问题得以解决.
试题解析:△DMN为等边三角形,理由如下:
∵△ABC为等边三角形,∴∠ACB=∠ABC=60°,∵DE//AB,DF∥AC,∴∠EDC=∠ABC=60°,∠FDB=∠ACB=60°,∴∠FDE=60°,△BDF、△EDC是等边三角形,∴BD=FD,ED=CD,∵∠BDE=∠FDC=120°,∴△BDE≌△FDC,∴∠BED=∠FCD,又∵∠NDE=∠MDC=60°,∴△NDE≌△MDC,∴DN=DM,∴△DMN是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径CD垂直于弦AB,垂足为点E,∠ACD=22.5°,若CD=6cm,则AB的长为( )
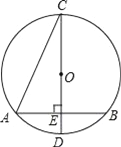
A. 4cm B. 3![]() cm C. 2
cm C. 2![]() cm D. 2
cm D. 2![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.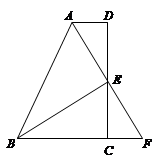
求证:
(1)AD=FC;
(2)AB=BC+AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 了解全市中学生对泰州“三个名城”含义的知晓度的情况,适合用抽样调查
B. 若甲组数据方差S甲2=0.39,乙组数据方差S乙2=0.27,则乙组数据比甲组数据稳定
C. 某种彩票中奖的概率是![]() ,买100张该种彩票一定会中奖
,买100张该种彩票一定会中奖
D. 数据﹣1、1.5、2、2、4的中位数是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中, ![]() C=2
C=2 ![]() B,点D是BC上一点,AD=6,且AD
B,点D是BC上一点,AD=6,且AD ![]() AB,点E是BD上的点,AE=
AB,点E是BD上的点,AE= ![]() BD,AC=5,贝AB的长度为 .
BD,AC=5,贝AB的长度为 . 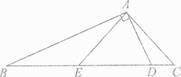
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com