
分析 当抛物线与x轴有两个交点时,只要满足x=-1和x=1时的函数值异号;当抛物线与x轴有一个交点时,只需要对应的一元二次方程的判别式等于0即可;从而可分别得到关于m的不等式或方程,可求得答案.
解答 解:∵y=2x2+3x+m,
∴当x=-1时,y=m-1,当x=1时,y=m+5,
令y=0可得2x2+3x+m=0,其判别式为△=9-8m.
当抛物线与x轴有两个交点时,
需满足$\left\{\begin{array}{l}{△>0}\\{(m-1)(m+5)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{9-8m>0}\\{(m-1)(m+5)}\end{array}\right.$,解得-5<m<1;
当抛物线与x轴只有一个交点时,
∵抛物线对称轴为x=-$\frac{3}{4}$,
∴其对称轴满足-1<x<1,
∴只需要△=0即可,即9-8m=0,解得m=$\frac{9}{8}$;
综上可知m的取值范围为-5<m<1或m=$\frac{9}{8}$,
故答案为:-5<m<1或m=$\frac{9}{8}$.
点评 本题主要考查抛物线与x轴的交点,掌握抛物线与x轴的交点与对应一元二次方程根的关系是解题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
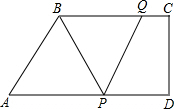 如图,在梯形ABCD中,∠D=90°,BC∥AD.BC=20,DC=16,AD=30,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
如图,在梯形ABCD中,∠D=90°,BC∥AD.BC=20,DC=16,AD=30,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
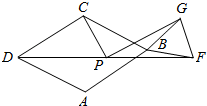 如图,菱形ABCD中,∠ABC=60°,BF=BG,∠GBF=60°,P是DF的中点,连接PG、PC.若∠CPD=60°,PG=$\frac{5\sqrt{3}}{2}$,DF=8,则菱形的边长为$\frac{7}{2}$.
如图,菱形ABCD中,∠ABC=60°,BF=BG,∠GBF=60°,P是DF的中点,连接PG、PC.若∠CPD=60°,PG=$\frac{5\sqrt{3}}{2}$,DF=8,则菱形的边长为$\frac{7}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
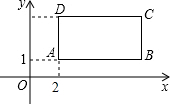 如图,长方形ABCD在坐标平面内,点A的坐标是A(2,1),且边AB、CD与x轴平行,边AD、BC与y轴平行,点B、C的坐标分别为B(a,1),C(a,c),且a、c满足关系式.c=$\sqrt{a-6}$+$\sqrt{6-a}$+3
如图,长方形ABCD在坐标平面内,点A的坐标是A(2,1),且边AB、CD与x轴平行,边AD、BC与y轴平行,点B、C的坐标分别为B(a,1),C(a,c),且a、c满足关系式.c=$\sqrt{a-6}$+$\sqrt{6-a}$+3查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某种自动卸货时的示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A的距离为(2$\sqrt{3}$+2)米.试求货车卸货时举升杠杆OB的长.
如图是某种自动卸货时的示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A的距离为(2$\sqrt{3}$+2)米.试求货车卸货时举升杠杆OB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com