
【题目】已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

【答案】(1)∠BAD=∠CAE;(2)∠DCE=60°,不发生变化,理由见解析.
【解析】
(1)由等边三角形的性质得出∠BAC=∠DAE,(2)由△ABC和△ADE是等边三角形可以得出AB=BC=AC,AD=AE,∠ABC=∠ACB=∠BAC=∠DAE=60°,得出∠ACD=120°,再证明△ABD≌△ACE,得出∠ABD=∠ACE=120°,即可得出结论;
(1)∠BAD=∠CAE
(2)∠DCE=60°,不发生变化 .理由如下:
∵△ABC是等边三角形,△ADE是等边三角形,
∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AB=AC,AD=AE,
∴∠ACD=120°,∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE
易证△ABD≌△ACE(SAS),
∴∠ACE=∠B=60°,
∴∠DCE=∠ACD-∠ACE=120°-60°=60°


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图信息,L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象,问

(1)在刚出发时我公安快艇距走私船多少海里?
(2)计算走私船与公安快艇的速度分别是多少?
(3)写出L1,L2的解析式
(4)问6分钟时两艇相距几海里.
(5)猜想,公安快艇能否追上走私船,若能追上,那么在几分钟追上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】附加题:
观察下列等式: ![]() ,
, ![]() ,
, ![]() ,
,
将以上三个等式两边分别相加得:![]() .
.
(1)直接写出下列各式的计算结果: ![]() =
=
(2)猜想并写出: ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ).
).
(3)探究并解方程: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李和小陆从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示,根据图中的信息,有下列说法:
(1)他们都行驶了20 km;
(2)小陆全程共用了1.5h;
(3)小李和小陆相遇后,小李的速度小于小陆的速度
(4)小李在途中停留了0.5h。
其中正确的有
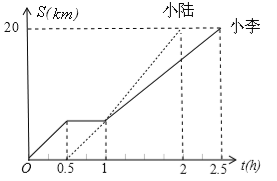
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中画出直线y=![]() x+1的图象,并根据图象回答下列问题:
x+1的图象,并根据图象回答下列问题:
(1)写出直线与x轴、y轴的交点坐标;
(2)求出直线与坐标轴围成的三角形的面积;
(3)若直线y=kx+b与直线y=![]() x+1关于y轴对称,求k,b的值.
x+1关于y轴对称,求k,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD. 
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=AD=8,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?试说明你找出的规律的正确性.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com