
【题目】如图,已知直线 ![]() 与x轴、y轴相交于P、Q两点,与y=
与x轴、y轴相交于P、Q两点,与y=![]() 的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+
的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB. 给出下列结论: ①k1k2<0;②m+![]() n=0; ③S△AOP= S△BOQ;④不等式k1x+b>
n=0; ③S△AOP= S△BOQ;④不等式k1x+b>![]() 的解集是x<-2或0<x<1,其中正确的结论的序号是 .
的解集是x<-2或0<x<1,其中正确的结论的序号是 .
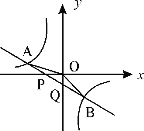
【答案】②③④.
【解析】
试题分析:①由直线 ![]() 的图像在二、四象限,知k1<0;y=
的图像在二、四象限,知k1<0;y=![]() 的图像在二、四象限,知k2<0;因此k1k2>0,所以①错误;②A,B两点在y=
的图像在二、四象限,知k2<0;因此k1k2>0,所以①错误;②A,B两点在y=![]() 的图像上,故将A(-2,m)、B(1,n)代入,得m=
的图像上,故将A(-2,m)、B(1,n)代入,得m=![]() ,n= k2;从而得出m+
,n= k2;从而得出m+![]() n=0,故②正确;③令x=0,则y=b,所以Q(0,b),则S△BOQ=
n=0,故②正确;③令x=0,则y=b,所以Q(0,b),则S△BOQ=![]() ×1×|b|= -
×1×|b|= -![]() b;将A(-2,m)、B(1,n)分别代入
b;将A(-2,m)、B(1,n)分别代入![]() ,解得k1=
,解得k1=![]() ,所以y=
,所以y=![]() x+b;令y=0,则x=-
x+b;令y=0,则x=-![]() b,所以P(-
b,所以P(-![]() b,0),则S△AOP=
b,0),则S△AOP=![]() ×|-2|×|-
×|-2|×|-![]() b|= -
b|= -![]() b;所以S△AOP= S△BOQ,故③正确;④由图像知,在A点左边,不等式k1x+b的图像在
b;所以S△AOP= S△BOQ,故③正确;④由图像知,在A点左边,不等式k1x+b的图像在![]() 的图像的上边,故满足k1x+b>
的图像的上边,故满足k1x+b>![]() ;在Q点与A点之间,不等式k1x+b的图像在
;在Q点与A点之间,不等式k1x+b的图像在![]() 的图像的上边,故满足k1x+b>
的图像的上边,故满足k1x+b>![]() ;因此不等式k1x+b>
;因此不等式k1x+b>![]() 的解集是x<-2或0<x<1. 故④正确.
的解集是x<-2或0<x<1. 故④正确.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
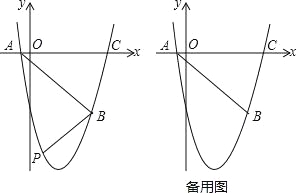
【题目】如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】事件A:某人上班乘车,刚到车站车就到了;事件B:掷一枚骰子,向上一面的点数不大于6.则正确的说法是( )
A.只有事件A是随机事件
B.只有事件B是随机事件
C.都是随机事件
D.都不是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下面的有理数填在相应的大括号里:(★友情提示:将各数用逗号分开)
15,﹣ ![]() ,0, ﹣30,﹣0.15,﹣128,
,0, ﹣30,﹣0.15,﹣128, ![]() , +20,﹣2.6
, +20,﹣2.6
正数集合{ ﹜;
负数集合﹛ ﹜;
整数集合﹛ ﹜;
非负数集合﹛ ﹜.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若⊙O的半径为R,直线l与⊙O有公共点,若圆心到直线l的距离为d,则d与R的大小关系是( ).
A. d>R B. d<R C. d≥R D. d≤R
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式不能使用平方差公式的是( )
A.(2a+b)(2a﹣b)
B.(﹣2a+b)(b﹣2a)
C.(﹣2a+b)(﹣2a﹣b)
D.(2a﹣b)﹣(2a﹣b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com