
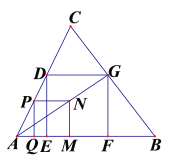
【题目】如图,正方形PQMN在△ABC内,点P在AC上,点Q、M在AB上,N在△ABC内,连接AN并延长交BC于G,过G点作GD∥AB交AC于D,过D、G分别作DE ⊥AB,GF⊥AB,垂足分别为E、F.
(1)求证:DG=GF;
(2)若AB=10,S△ABC=40,试求四边形DEFG的面积.
【答案】(1)见解析; (2)![]()
【解析】
(1)根据相似三角形的判定定理,证得△AMN∽△AFG,△APN∽△ADG,再根据相似三角形的对应边成比例可得![]() ,
,![]() ,根据正方形的性质判断PN=NM,进而求证DG=GF;
,根据正方形的性质判断PN=NM,进而求证DG=GF;
(2)如图,过点C作△ABC的高CI分别交DG、AB于点H、I,根据三角形的面积公式求出CI,由题(1)证得四边形DEFG是正方形,根据正方形的性质可得DE=EF=FG=DG,DE⊥AB,GF⊥AB,再设正方形DEFG的边长为x,根据三角形的面积公式求出S△CDG、S△ADE、S△BFG,根据正方形的面积公式可得:S正方形DEFG,由S△ABC=S△CDG+S△ADE+S△BFG+S正方形DEFG可列关于x的方程,解方程即可求得x,进而可求四边形DEFG的面积.
(1)∵DE⊥AB,GF⊥AB,GD∥AB
∴DE⊥DG,GF⊥DG
∴∠DEF=∠EFG=∠DGF=∠EDG=90°
∴四边形DGFE是矩形,
∵四边形PQME是正方形,
∴∠NMQ=90°,NM⊥AB,PN=NM
∴NM∥GF
∴△AMN∽△AFG
∴![]()
同理可得:![]()
∴![]()
∵PN=NM
∴GF=DG
(2)如图,过点C作△ABC的高CI分别交DG、AB于点H、I,
易知CI⊥AB,CH⊥DG
∵AB=10,S△ABC=40,
![]()
∴CI=8,
由(1)知:四边形DEFG是矩形,且GF=DG
∴四边形DEFG是正方形
∴DE=EF=GF=DG=HI,DE⊥AB,GF⊥AB,
设DE=EF=GF=DG=HI=x,
则CH=CI-HI=8-x,AE+BF=AB-EF=10-x,
∴S△CDG=![]() DG·CH=
DG·CH=![]() ,
,
S△ADE=![]() AE·DE=
AE·DE=![]() ,S△BFG=
,S△BFG=![]() BF·GF=
BF·GF=![]() ,
,
S正方形DEFG=![]() ,
,
∴S△ADE+S△BFG=![]() =
=![]() ,
,
∵S△CDG+S△ADE+S△BFG+S正方形DEFG=S△ABC=40,
∴![]() +
+![]() +
+![]() =40,
=40,
整理得:![]() ,
,
解得:![]() ,
,
∴S四边形DEFG =![]() =
=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
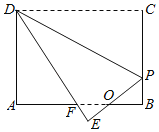
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则BF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场今年2月份营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.若设商场3月份到5月份营业额的月平均增长率为x,则下面列出的方程中正确的是( )
A.633.6(1+x)2=400(1+10%)B.633.6(1+2x)2=400×(1010%)
C.400×(1+10%)(1+2x)2=633.6D.400×(1+10%)(1+x)2=633.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌手机销售公司有营销员14人,销售部为制定营销人员月销售手机定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 165 | 80 | 50 | 40 |
人 数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)求这14位营销员该月销售该品牌手机的平均数、中位数和众数.
(2)销售部经理把每位营销员月销售量定为100台,你认为是否合理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
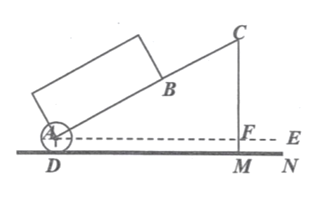
【题目】一种拉杆式旅行箱的示意图如图所示,箱体长![]() ,拉杆最大伸长距离
,拉杆最大伸长距离![]() ,(点
,(点![]() 在同一条直线上),在箱体的底端装有一圆形滚轮
在同一条直线上),在箱体的底端装有一圆形滚轮![]() 与水平地面切于点
与水平地面切于点![]() 某一时刻,点
某一时刻,点![]() 距离水平面
距离水平面![]() ,点
,点![]() 距离水平面
距离水平面![]() .
.
(1)求圆形滚轮的半径![]() 的长;
的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点![]() 处且拉杆达到最大延伸距离时,点
处且拉杆达到最大延伸距离时,点![]() 距离水平地面
距离水平地面![]() ,求此时拉杆箱与水平面
,求此时拉杆箱与水平面![]() 所成角
所成角![]() 的大小(精确到
的大小(精确到![]() ,参考数据:
,参考数据:![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,点D在AC上(CD<![]() AC),连接BD.操作:以A为圆心,AD长为半径画弧,交BD于点E,连接AE.
AC),连接BD.操作:以A为圆心,AD长为半径画弧,交BD于点E,连接AE.
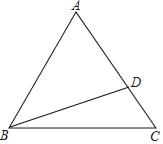
(1)请补全图形,探究∠BAE、∠CBD之间的数量关系,并证明你的结论;
(2)把BD绕点D顺时针旋转60°,交AE于点F,若EF=mAF,求![]() 的值(用含m的式子表示).
的值(用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图四边形OACB是菱形,OB在X轴的正半轴上,sin∠AOB=![]() .反比例函数y=
.反比例函数y=![]() 在第一象限图象经过点A,与BC交于点F.S△AOF=
在第一象限图象经过点A,与BC交于点F.S△AOF=![]() ,则k=( )
,则k=( )
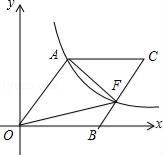
A. 15 B. 13 C. 12 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com