
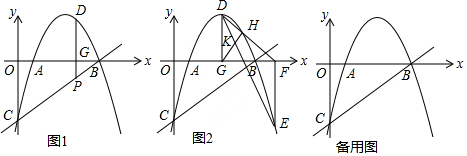
���� ��1��������B��10��0����C��0��-5������B��C�����������y=ax2+3x+c����$\left\{\begin{array}{l}{c=-5}\\{100a+30-5=0}\end{array}\right.$���ⷽ���鼴�ɽ�����⣮
��2����ͼ1�У���D��m��-$\frac{1}{4}$m2+3m-5������P��m��$\frac{1}{2}$m-5��������DG=2PG���г����̼��ɣ�
��3����ͼ2�У��ӳ�GH��EF���ӳ�����M��DE��GF��J������DM����E��m��-$\frac{1}{4}$m2+3m-5�����ɡ�DME�ס�DGF���Ƴ���DEM=��DFG=��KGJ���Ƴ���GKJ=��EFJ=90�㣬���ɡ�DKG�ס�EMD���õ�$\frac{DK}{GK}$=$\frac{EM}{DM}$=$\frac{3}{2}$���г����̼��ɽ�����⣬���ݶԳ����������һ����E���꼴�ɣ�
��� �⣺��1��������B��10��0����C��0��-5����
��B��C�����������y=ax2+3x+c����$\left\{\begin{array}{l}{c=-5}\\{100a+30-5=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{c=-5}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{1}{4}$x2+3x-5��
��2����ͼ1�У���D��m��-$\frac{1}{4}$m2+3m-5������P��m��$\frac{1}{2}$m-5����
��DG=2GP��
��-$\frac{1}{4}$m2+3m-5=2��5-$\frac{1}{2}$m����
��m=6��10����������
���D���꣨6��4����
��3����ͼ2�У��ӳ�GH��EF���ӳ�����M��DE��GF��J������DM����E��m��-$\frac{1}{4}$m2+3m-5����
��HD=HF=HG��
���HGF=��HFG��
�ߡ�HGF+��FMG=90�㣬��HFG+��HFM=90�㣬
���HFM=��HMF��
��HM=HF��
��DH=HF=HM=HG��
���ı���DGFM�Ǿ��Σ�
��DM=GF=m-6��DG=FM=4��EM=4+$\frac{1}{4}$m2-3m+5��
��$\frac{DM}{DG}$=$\frac{m-6}{4}$��$\frac{EM}{FG}$=$\frac{\frac{1}{4}{m}^{2}-3m+9}{m-6}$=$\frac{m-6}{4}$��
��$\frac{DM}{DG}$=$\frac{EM}{FG}$���ߡ�DME=��DGF=90�㣬
���DME�ס�DGF��
���DEM=��DFG=��KGJ��
�ߡ�KJG=��EJF��
���GKJ=��EFJ=90�㣬
���DKG=��DME���ߡ�KDG=��DEM��
���DKG�ס�EMD��
��$\frac{DK}{GK}$=$\frac{EM}{DM}$=$\frac{3}{2}$��
��$\frac{\frac{1}{4}{m}^{2}-3m+9}{m-6}$=$\frac{3}{2}$��
��m=12��6����������
���E���꣨12��-5�������ݶԳ��Կ�֪����E�ڶԳ������ʱ��Ҳ������������ʱE��0��-5����
������������E��������12��-5����0��-5����
���� ���⿼����κ����ۺ��⡢����ϵ���������������ε��ж������ʡ����ε��ж������ʵ�֪ʶ������Ĺؼ����������������ε����ʣ��Ƴ�DE��HG���������������ν�ϵ�˼�룬�������������β������֣����Ǹ��ѵ㣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
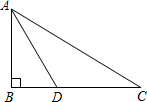 ��ͼ����ABC�У���B=90�㣬AB=3��BD=3��ADΪ��BAC�Ľ�ƽ���ߣ����D��AC�ľ���Ϊ3��
��ͼ����ABC�У���B=90�㣬AB=3��BD=3��ADΪ��BAC�Ľ�ƽ���ߣ����D��AC�ľ���Ϊ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
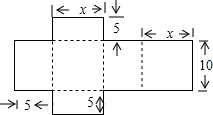 ��ͼ����֪ij�������չ��ͼ�����Ϊ310cm2������ͼ�����ݿ��г�����x��һԪһ�η���Ϊ2����10x+5x+5��10��=310��x��ֵΪ7��
��ͼ����֪ij�������չ��ͼ�����Ϊ310cm2������ͼ�����ݿ��г�����x��һԪһ�η���Ϊ2����10x+5x+5��10��=310��x��ֵΪ7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
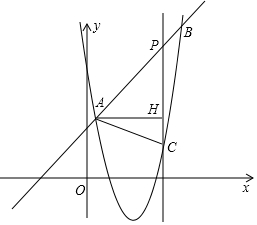 ��ͼ��ֱ��y=x+2��������y=ax2+bx+6�ཻ��A��$\frac{1}{2}$��$\frac{5}{2}$����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x�ᣬ���������ڵ�C��
��ͼ��ֱ��y=x+2��������y=ax2+bx+6�ཻ��A��$\frac{1}{2}$��$\frac{5}{2}$����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x�ᣬ���������ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
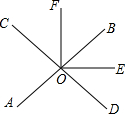 ��ͼ��ֱ��AB��CD�ཻ�ڵ�O��OEƽ�֡�BOD��OF��OE�ڵ�O������AOC=60�㣬���BOF�Ķ�����
��ͼ��ֱ��AB��CD�ཻ�ڵ�O��OEƽ�֡�BOD��OF��OE�ڵ�O������AOC=60�㣬���BOF�Ķ������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com