
【题目】在平面直角坐标系中,O为坐标原点,直线y=kx﹣2k(k<0)的与y轴交于点A,与x轴交于点B.
(1)如图1,求点B的坐标;
(2)如图2,第一象限内的点C在经过B点的直线y=-![]() x+b上,CD⊥y轴于点D,连接BD,若S△ABD=2k+2,求C点的坐标(用含k的式子表示);
x+b上,CD⊥y轴于点D,连接BD,若S△ABD=2k+2,求C点的坐标(用含k的式子表示);
(3)如图3,在(2)的条件下,连接OC,交直线AB于点E,若3∠ABD﹣∠BCO=45°,求点E的坐标.
【答案】(1)B(2,0);(2)C(2﹣2k,2);(3)E(![]() ,
,![]() )
)
【解析】
(1)令y=kx﹣2k=0,解方程即求得点B坐标.
(2)求点A坐标(用含k的式子),把点B坐标代入直线y=-![]() x+b求得b=
x+b求得b=![]() .由
.由![]() 求得点D纵坐标为2,所以点C纵坐标也为2,把y=2代入直线y=-
求得点D纵坐标为2,所以点C纵坐标也为2,把y=2代入直线y=-![]() x+
x+![]() ,即求得点C横坐标.
,即求得点C横坐标.
(3)如图,过点C作CH⊥x轴于点H,在CD上取一点J,使得AJ=CJ,连接AJ,AC.首先证明∠AJD=∠COD,根据tan∠AJD=tan∠COD,构建方程求出k,再求出直线OC,AB的解析式,构建方程组确定交点E的坐标即可.
解:(1)∵直线y=kx﹣2k中,kx﹣2k=0时,解得:x=2
∴B(2,0)
(2)∵x=0时,y=kx﹣2k=﹣2k
∴A(0,﹣2k)
∵点B(2,0)在直线y=-![]() x+b上
x+b上
∴﹣![]() +b=0
+b=0
∴b=![]() ,直线解析式为y=-
,直线解析式为y=-![]() x+
x+![]()
∵![]()
∴![]()
∵CD⊥y轴于点D
∴![]()
∵点C在直线y=-![]() x+
x+![]() 上
上
∴-![]() x+
x+![]() =2,解得x=2﹣2k
=2,解得x=2﹣2k
∴C(2﹣2k,2)
(3)如图,过点C作CH⊥x轴于点H,在CD上取一点J,使得AJ=CJ,连接AJ,AC.
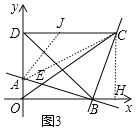
由(2)可知:CH=OB=2,∠BOA=∠CHB=90°,BH=OA=﹣2k,
∴△CHB≌△BOA(SAS),
∴BC=BA,
∵∠ABC=90°,
∴∠ACB=45°,
∵∠ADC=∠ABC=90°,
∴∠ADC+∠ABC=180°,
∴A,D,C,B四点共圆,
∴∠ABD=∠ACD,
∵3∠ABD﹣∠BCO=45°,∠BCO=45°﹣∠ACO,
∴3∠ACD﹣(45°﹣∠ACO)=45°,
∴3∠ACD+∠AOC=90°,
∵∠DOC+∠ACD+∠ACO=90°,
∴∠DOC=2∠ACD,
∵JA=JC,
∴∠JCA=∠JAC,
∵∠AJD=∠JAC+∠JCA,
∴∠AJD=2∠DCA=∠COD,
设AJ=JC=x,在Rt△ADJ中,∵AJ2=AD2+DJ2,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
∵∠AJD=∠COD,
∴tan∠AJD=tan∠COD,
∴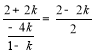 ,
,
解得![]() ,
,
∴A(0,![]() ),C(
),C(![]() ,2),
,2),
∴直线OC的解析式为y=![]() x,
x,
直线AB的解析式为![]() ,
,
由 ,解得
,解得![]() ,
,
∴E(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】嘉善县将开展以“珍爱生命,铁拳护航”为主题的交通知识竞赛,某校对参加选拔赛的若干名同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的频数统计表和扇形统计图
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合计 | 1 |
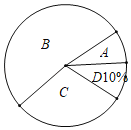
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应圆心角的度数;
(3)“A等级”的4名同学中有3名男生和1名女生,现从中随机挑选2名同学代表学校参加全县比赛,请用树状图法或列表法求出恰好选中“一男一女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
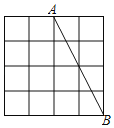
【题目】如图,正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上,请按要求画出图形并计算.
(1)以线段AB为一腰的等腰△ABC,点C在小正方形的顶点上,且S△ABC=6;
(2)以BC为对角线作平行四边形BDCE,点D,E均在小正方形的顶点上,且∠ABD=45°;
(3)连接DE,请直接写出线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片分别写有数字﹣1、﹣3、4、6,将这些卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字大于0的概率是______;
(2)从中任意抽取1张,并将卡片上的数字记作二次函数y=ax2+bx中的a,再从余下的卡片中任意抽取1张,并将卡片上的数字记作二次函数y=ax2+bx中的b,利用树状图或表格的方法,求出这个二次函数图象的对称轴在y轴右侧的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,过点(0,1)和(﹣1,0),给出以下结论:①ab<0;②4a+c<1+b2;③0<c+b+a<2;④0<b<2;⑤当x>﹣1时,y>0;⑥8a+7b+2c﹣9<0其中正确结论的个数是( )
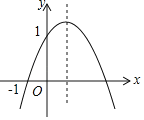
A.6B.5C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com