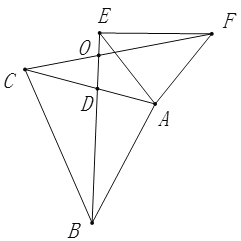
【题目】如图，已知在
和
中，
交
于
点，
求证:
；
当
时，求
的度数．
【答案】（1）证明见解析；（2）∠BOC=70°．
【解析】
（1）求出∠BAE=∠CAF，根据SAS推出△BAE≌△CAF，推出BE=CF即可；
（2）求出∠EBA+∠BDA=110°，求出∠ACF+∠CDO=110°，即可得出答案；
（1）∵∠CAB=∠EAF，
∴∠CAB+∠CAE=∠EAF+∠CAE，
∴∠BAE=∠CAF，
在△BAE和△CAF中，
，
∴△BAE≌△CAF（SAS），
∴BE=CF；
（2）∵△BAE≌△CAF，
∴∠EBA=∠FCA，
∵∠CAB=70°，
∴∠EBA+∠BDA=180°-70°=110°，
∵∠BDA=∠CDE，∠EBA=∠FCA，
∴∠ACF+∠CDE=110°，
∴∠BOC=180°-（∠ACF+∠CDE）=180°-110°=70°．
科目：初中数学 来源： 题型：
【题目】如图所示，已知A（
，y1），B(2,y2)为反比例函数
图像上的两点，动点P(x，0)在x正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）
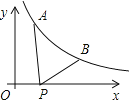
A. (，0) B. (1,0) C. (
,0) D. (
,0)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，E、F、 G、H分别为四边形ABCD四边之中点．
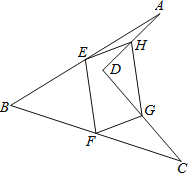
(1)求证：四边形EFGH为平行四边形；
(2)当AC、BD满足______时，四边形EFGH为矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
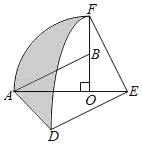
【题目】如图，在Rt△AOB中，∠AOB=90°，OA=2，OB=1，将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE，将线段EF绕点E逆时针旋转90°后得到线段ED，分別以O、E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分的面积是__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AD=2，AB=3，过点A，C作相距为2的平行线段AE，CF，分别交CD，AB于点E，F，则DE的长是（ ）
A. 
B. 
C. 1 D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．
（1）请你根据已经学过的知识求出下面星形图（1）中∠A+∠B+∠C+∠D+∠E的度数；
（2）若对图（1）中星形截去一个角，如图（2），请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数；
（3）若再对图（2）中的角进一步截去，你能由题（2）中所得的方法或规律，猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗？只要写出结论，不需要写出解题过程）
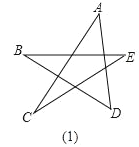
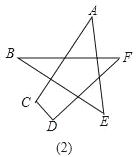
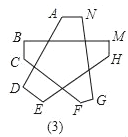
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）问题发现
如图1，在Rt△ABC中，∠A=90°，
=1，点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接 CD．
（1）①求
的值；②求∠ACD的度数．
（2）拓展探究
如图 2，在Rt△ABC中，∠A=90°，=k．点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD，请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系，并说明理由．
（3）解决问题
如图 3，在△ABC中，∠B=45°，AB=4
，BC=12，P 是边BC上一动点（不与点B重合），∠PAD=∠BAC，∠APD=∠B，连接CD．若 PA=5，请直接写出CD的长．
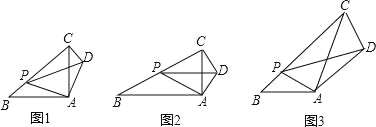
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小黄站在河岸上的
点，看见河里有一小船沿垂直于岸边的方向划过来．此时，测得小船
的俯角是
，若小黄的眼睛与地面的距离
是
米，
米，
平行于
所在的直线，迎水坡
的坡度为
，坡长
米，则此时小船到岸边的距离
的长为（ ）米．（
，结果保留两位有效数字）
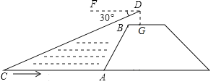
A. 11 B. 8.5 C. 7.2 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
