
【题目】如图所示,AB是⊙O的直径,AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP、AF. 
求证:
(1)AF∥BE;
(2)△ACP∽△FCA;
(3)CP=AE.
【答案】
(1)证明:∵∠B、∠F同对劣弧AP,
∴∠B=∠F,
∵BO=PO,
∴∠B=∠BPO,
∴∠F=∠BPF,
∴AF∥BE.
(2)证明:∵AC切⊙O于点A,AB是⊙O的直径,
∴∠BAC=90°.
∵AB是⊙O的直径,
∴∠BPA=90°,
∴∠EAP=90°﹣∠BEA,∠B=90°﹣∠BEA,
∴∠EAP=∠B=∠F,
又∠C=∠C,
∴△ACP∽△FCA.
(3)证明:∵∠CPE=∠BPO=∠B=∠EAP,∠C=∠C.
∴△PCE∽△ACP
∴ ![]() ,
,
∵∠EAP=∠B,∠EPA=∠APB=90°,
∴△EAP∽△ABP.
∴ ![]() ,
,
又AC=AB,
∴ ![]() ,
,
于是有 ![]() .
.
∴CP=AE.
【解析】(1)由∠B、∠F同对劣弧AP,可知两角的关系,又因BO=PO,△BOP是等腰三角形,求出∠F=∠BPF,得出结论;(2)AC切⊙O于点A,AB是⊙O的直径,证明∠EAP=∠B,故△ACP∽△FCA;(3)由∠CPE=∠BPO=∠B=∠EAP,∠C=∠C,证得三角形相似,列出比例式,可得到等式成立.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】三角形中,一个内角α是另一个内角β的两倍时,我们称此三角形是“特征三角形”,其中α为“特征角”.如果一个“特征三角形”的“特征角”为102°,那么这个“特征三角形”的最小内角为___________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是必然事件的是( )
A.足球运动员射门一次,球射进球门B.随意翻开一本书,这页的页码是奇数
C.经过有交通信号灯的路口,遇到绿灯D.任意画一个三角形,其内角和是180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC= ![]() .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 . 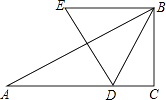
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.
(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果至少购买两种款式的书包共80个,那么女款书包最多能买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AE与CD相交于点B,射线BF平分∠ABC,射线BG在∠ABD内,
(1)若∠DBE的补角是它的余角的3倍,求∠DBE的度数;
(2)在(1)的件下,若∠DBG=∠ABG﹣33°,求∠ABG的度数;
(3)若∠FBG=100°,求∠ABG和∠DBG的度数的差.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y= ![]() (k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
(k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S. 
(1)求k的值;
(2)当S= ![]() 时,求P点的坐标;
时,求P点的坐标;
(3)写出S关于m的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com