
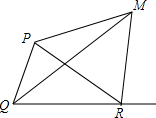
 如图,△PQR的外角∠PRN的平分线PM与内角∠PQR的平分线QM交于点M,∠QMR=40°,则∠RPM的度数为50°.
如图,△PQR的外角∠PRN的平分线PM与内角∠PQR的平分线QM交于点M,∠QMR=40°,则∠RPM的度数为50°. 分析 先根据角平分线的性质及三角形外角的性质求出∠QPR的度数,再作MA⊥QN,MB⊥PR,MC⊥QP的延长线于点C,由角平分线的性质得出MA=MB,MA=MC,故MB=MC,即M在∠RPC的平分线上,由角平分线的性质可得出结论.
解答 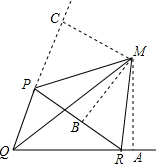 解:∵△PQR的外角∠PRN的平分线PM与内角∠PQR的平分线QM交于点M,
解:∵△PQR的外角∠PRN的平分线PM与内角∠PQR的平分线QM交于点M,
∴∠MQR=$\frac{1}{2}$∠PQR,
∠MRN=∠QMR+∠MQR=$\frac{1}{2}$(∠QPR+∠PQR)=∠QMR+$\frac{1}{2}$∠PQR.
∴$\frac{1}{2}$∠QPR+$\frac{1}{2}$∠PQR=∠QMR+$\frac{1}{2}$∠PQR,
∴∠QPR=2∠QMR=80°.
作MA⊥QN,MB⊥PR,MC⊥QP的延长线于点C.
∵MR和MQ是∠平分线,
∴MA=MB,MA=MC,
∴MB=MC,
∴M在∠RPC的平分线上,
∴∠RPM=$\frac{180°-∠QPR}{2}$=$\frac{180°-80°}{2}$=50°.
故答案为:50°.
点评 本题考查的是角平分线的性质,根据题意作出辅助线,利用角平分线的性质求解是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
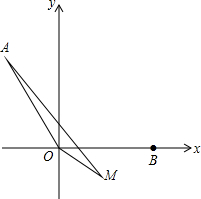 如图,在平面直角坐标系xOy中,点M(1,-$\frac{\sqrt{3}}{3}$),点A和x轴正半轴上的点B,满足AO=OB=2,∠AOB=120°.
如图,在平面直角坐标系xOy中,点M(1,-$\frac{\sqrt{3}}{3}$),点A和x轴正半轴上的点B,满足AO=OB=2,∠AOB=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com