
分析 根据规律得出结果的分子为原式中两分母之和;分母为两分母之积,据此可得答案.
解答 解:∵(-1)+(-$\frac{1}{2}$)=-$\frac{3}{2}$=-$\frac{1+2}{1×2}$;
(-$\frac{1}{2}$)+(-$\frac{1}{3}$)=-$\frac{5}{6}$=$-\frac{2+3}{2×3}$;
(-$\frac{1}{3}$)+(-$\frac{1}{4}$)=-$\frac{7}{12}$=-$\frac{3+4}{3×4}$;
…
∴(-$\frac{1}{12}$)+($-\frac{1}{13}$)=$-\frac{12+13}{12×13}$=$-\frac{25}{156}$;
(-$\frac{1}{n}$)+(-$\frac{1}{n+1}$)=-$\frac{n+n+1}{n(n+1)}$=-$\frac{2n+1}{{n}^{2}+n}$.
故答案为:$-\frac{25}{156}$,-$\frac{2n+1}{{n}^{2}+n}$.
点评 本题主要考查了数字的变化规律,根据已知得出分子,分母的变化是解答此题的关键.


科目:初中数学 来源: 题型:解答题
 如图,正三角形ABC的边长为2$\sqrt{3}$.
如图,正三角形ABC的边长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:解答题
某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中复习数学检测试卷(一)(解析版) 题型:单选题
如果 是二元一次方程,那么
是二元一次方程,那么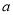 、
、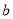 的值分别是( )
的值分别是( )
A. 3、1 B. 3、2 C. 2、1 D. 2、-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com