Question

12．如图，正方形ABCD的边长为4$\sqrt{5}$，E、F分别是AB、BC的中点，动点G从D点出发沿DE以每秒1个单位的速度向E点运动，设运动时间为t秒，当∠EGF=45°时，求t的值．

Answer 1

分析 如图，连接EF、DF，作FM⊥DE于M．先求出△DEF的面积，再求出高FM，利用勾股定理求出EM、DM，利用等腰三角形的性质求出DG即可解决问题．

解答 解：如图，连接EF、DF，作FM⊥DE于M．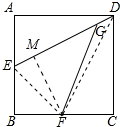

∵四边形ABCD是正方形，
∴AB=BC=CD=AD=4$\sqrt{5}$，
∵AE=EB=BF=FC=2$\sqrt{5}$，
∴ED=$\sqrt{A{D}^{2}+A{E}^{2}}$=10，EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=2$\sqrt{10}$，
∴S_△DEF=4$\sqrt{5}$×4$\sqrt{5}$-$\frac{1}{2}$×$2\sqrt{5}$×$4\sqrt{5}$-$\frac{1}{2}$×2$\sqrt{5}$×4$\sqrt{5}$-$\frac{1}{2}$×2$\sqrt{5}$×2$\sqrt{5}$=$\frac{1}{2}$×DE•FM，
∴FM=6，
在Rt△EFM中，EM=$\sqrt{E{F}^{2}-F{M}^{2}}$=2，
∴DM=DE-EM=8，
∵∠MGF=45°，
∴∠MGF=∠MFG=45°，
∴MG=FM=2，
∴DG=DM-MG=2，
∴t=2，
∴当t=2时，∠EGF=45°．

点评 本题考查正方形的性质、等腰直角三角形的性质、勾股定理等知识，解题的关键是学会利用分割法求三角形面积，学会添加常用辅助线，构造直角三角形，属于中考常考题型．