
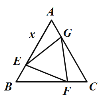
【题目】已知正![]() ABC的边长为2,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设
ABC的边长为2,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设![]() EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
A.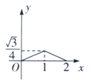 B.
B.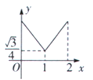 C.
C.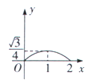 D.
D.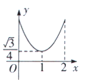
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2019年12月17日,我国第一艘国产航母“山东舰”在海南三亚交付海军.在民族复兴的路上我们伟大的祖国又前进了一大步!如图,“山东舰”在一次试水测试中,由东向西航行到达![]() 处时,测得小岛
处时,测得小岛![]() 位于距离航母30海里的北偏东37°方向.“山东舰”再向西匀速航行1.5小时后到达
位于距离航母30海里的北偏东37°方向.“山东舰”再向西匀速航行1.5小时后到达![]() 处,此时测得小岛
处,此时测得小岛![]() 位于航母的北偏东70°方向.
位于航母的北偏东70°方向.
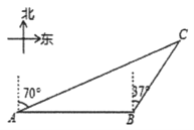
(1)![]() _______°;
_______°;
(2)求航母的速度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作AEDF.在点E从点B移动到点C的过程中,AEDF的面积( )

A.先变大后变小B.先变小后变大C.一直变大D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某测绘公司借助大型无人飞机航拍测绘.如图,无人飞机从C处放飞迅速爬升到点A处,继续水平飞行400米到达B处共需150秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.己知无人飞机的水平飞行速度为4米/秒,求这架无人飞机从C到A的爬升速度及水平飞行高度.(结果保留根号)
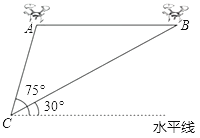
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
(1)甲船从C处出发追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB-BC→CD向点D运动设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所小示,则AD的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)

(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com