
【题目】点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将一直角的顶点放在点O处,∠MON=90°.

(1)如图1,当∠MON的一边OM与射线OB重合时,则∠NOC=_________;
(2)将∠MON绕点O逆时针运动至图2时,若∠MOC=15°,则∠BOM=______;∠AON=_______.
(3)在上述∠MON从图1运动到图3的位置过程中,当∠MON的边OM所在直线恰好平分∠AOC时,求此时∠NOC是多少度?
【答案】(1)150°;(2)45°,135°;(3)30°.
【解析】
(1)由∠AOC:∠BOC=2:1,根据平角的定义可求出∠AOC、∠BOC的度数,根据角的和差关系即可求出∠NOC的度数;
(2)根据∠BOC和∠MOC的度数可求出∠BOM的度数,根据角的和差关系即可求出∠BOM的度数,根据∠MON=90°可求出∠NOB的度数,根据平角的定义即可求出∠AON的度数;
(3)利用角平分线的定义可求出∠MOC的度数,进而可求出∠NOC的度数.
(1)∵∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=180°×![]() =120°,∠BOC=180°×
=120°,∠BOC=180°×![]() =60°,
=60°,
∵∠MON=90°,
∴∠NOC=∠BOC+∠MON=90°+60°=150°.
故答案为:150°
(2)由(1)可知:∠BOC=60°,
∵∠MOC=15°,
∴∠BOM=∠BOC-∠MOC=60°-15°=45°,
∵∠MON=90°,
∴∠BON=90°-∠BOM=45°,
∴∠AON=180°-∠AON=135°,
故答案为:45°,135°
(3)由(1)可知:∠AOC=120°,∠BOC=60°,
∵OM平分∠AOC,
∴∠COM=![]() ∠AOC=60°,
∠AOC=60°,
∵∠MON=90°,
∴∠NOC=∠MON-∠COM=90°-60°=30°.


科目:初中数学 来源: 题型:
【题目】为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价l80元,售价320元;乙种服装每件进价l50元,售价280元.
(1)若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?
(2)该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0<a<20)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划投入50万元,开发并生产甲乙两种产品,根据市场调查预计甲产品的年获利y1(万元)与投入资金x(万元)成正比例,乙产品的年获利y2(万元)与投入资金x(万元)的平方成正比例,设该公司投入乙产品x(万元),两种产品的年总获利为y万元(x≥0),得到了表中的数据.
x(万元) | 20 | 30 |
y(万元) | 10 | 13 |
(1)求y与x的函数关系式;
(2)该公司至少可获得多少利润?请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议,使他能获得最大利润,并求出最大利润是多少?
(3)若从年总利润扣除投入乙产品资金的a倍(a≤1)后,剩余利润随x增大而减小,求a的取值
范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )

A.  B.
B. 
C.  D.
D. 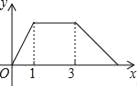
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C在同一直线上,M、N分别是AB,BC的中点.
(1)若AB=20,BC =8,求MN的长;
(2)若AB =a,BC =8,求MN的长;
(3)若AB =a,BC =b,求MN的长;
(4)从(1)(2)(3)的结果中能得到什么结论?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图①,若线段AB在数轴上,A、B两点表示的数分别为![]() 和
和![]() (
(![]() ),则线段AB的长(点A到点B的距离)可表示为AB=
),则线段AB的长(点A到点B的距离)可表示为AB=![]() .
.
请用上面材料中的知识解答下面的问题:如图②,一个点从数轴的原点开始,先向左移动2cm到达P点,再向右移动7cm到达Q点,用1个单位长度表示1cm.


(1)请你在图②的数轴上表示出P,Q两点的位置;
(2)若将图②中的点P向左移动![]() cm,点Q向右移动
cm,点Q向右移动![]() cm,则移动后点P、点Q表示的数分别为多少?并求此时线段PQ的长.(用含
cm,则移动后点P、点Q表示的数分别为多少?并求此时线段PQ的长.(用含![]() 的代数式表示);
的代数式表示);
(3)若P、Q两点分别从第⑴问标出的位置开始,分别以每秒2个单位和1个单位的速度同时向数轴的正方向运动,设运动时间为![]() (秒),当
(秒),当![]() 为多少时PQ=2cm?
为多少时PQ=2cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一定角度后,点
顺时针旋转一定角度后,点![]() 的对应点恰好与点
的对应点恰好与点![]() 重合,得到
重合,得到![]() .
.

(1)请求出旋转角的度数;
(2)请判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若![]() ,
,![]() ,试求出四边形
,试求出四边形![]() 的对角线
的对角线![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com