
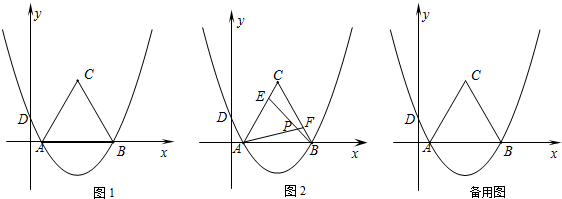
分析 (1)先设出抛物线的解析式,然后将已知点的坐标代入求解即可;
(2)过点C作CK⊥x轴,垂足为K.先求得三角形ABC的面积,从而得到△ABM的面积,依据三角形的面积公式可求得点M的纵坐标为4,由点M在抛物线可知可知y=4,从而可求得对应的x的值,于是得到点M的坐标;
(3)①先证明依据SAS△BEC≌△AFB,由全等三角形的性质可得到AF=BE,接下来证明∠FAB+∠ABP=∠ABC,最后依据三角形的内角和定理可求得∠APB的度数;②如图3所示:设$\widehat{AB}$所在圆的圆心为M,点H在圆M上,连接AM、BM、AH、BH,过点M作MG⊥AB,垂足为G.依据圆的内角四边形的性质和圆周角定理可求得∠AMB的长,接下来,依据等腰三角形三线合一的性质可得到AG=3,∠AMG=60°,然后依据特殊锐角三角函数值可求得AM的长,最后依据扇形的弧长公式求解即可;如图4所示:当AE=BF时.依据SAS可证明△AEB≌△BAF,从而得到∠PAB=∠PBA,故此可知点P在AB的垂直平分线上,最后依据特殊锐角三角函数求得CN的长即可.
解答 解:(1)设抛物线的解析式为y=ax2+bx+$\frac{7}{4}$.
∵将点A、B的坐标代入得:$\left\{\begin{array}{l}{49a+7b+\frac{7}{4}=0}\\{a+b+\frac{7}{4}=0}\end{array}\right.$,解得:a=$\frac{1}{4}$,b=-2,
∴抛物线的解析式为y=$\frac{1}{4}$x2-2x+$\frac{7}{4}$.
(2)存在点M使得S△AMB=$\frac{4\sqrt{3}}{9}$S△ABC.
如图1所示:过点C作CK⊥x轴,垂足为K.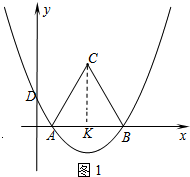
∵△ABC为等边三角形,
∴AB=BC=AC=6,∠ACB=60°.
∵CK⊥AB,
∴KA=BK=3,∠ACK=60°.
∴CK=3$\sqrt{3}$.
∴S△ABC=$\frac{1}{2}$AB•CK=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$.
∴S△ABM=$\frac{4\sqrt{3}}{9}$×$9\sqrt{3}$=12.
设M(x,$\frac{1}{4}$x2-2x+$\frac{7}{4}$).
∴$\frac{1}{2}$AB•|yM|=12,即$\frac{1}{2}$×6×($\frac{1}{4}$x2-2x+$\frac{7}{4}$)=12.
解得x1=9,x2=-1.
∴M1(9,4),M2(-1,4).
(3)①AF=BE,∠APB=120°.
理由:如图2所示;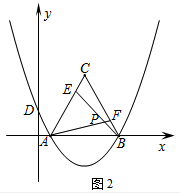
∵△ABC为等边三角形,
∴BC=AB,∠C=∠ABF.
∵在△BEC和△AFB中$\left\{\begin{array}{l}{BC=AB}\\{∠C=∠ABF}\\{CE=BF}\end{array}\right.$,
∴△BEC≌△AFB.
∴AF=BE,∠CBE=∠BAF.
∴∠FAB+∠ABP=∠ABP+∠CBE=∠ABC=60°.
∴∠APB=180°-∠PAB-∠ABP=180°-60°=120°.
②如图3所示:当CE=FB时.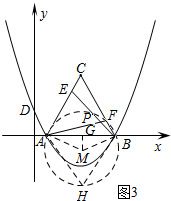
∵由①可知:∠APB=120°,
∴点P的运动轨迹是一条弧.
设$\widehat{AB}$所在圆的圆心为M,点H在圆M上,连接AM、BM、AH、BH,过点M作MG⊥AB,垂足为G.
∵∠APB=120°,
∴∠AHB=60°.
∴∠AMB=120°.
∵AM=MB,MG⊥AB,
∴AG=BG=3,∠AMG=∠BMG=60°.
∴$\frac{AG}{AM}=\frac{\sqrt{3}}{2}$,即$\frac{3}{AM}=\frac{\sqrt{3}}{2}$.
∴AM=2$\sqrt{3}$.
∴点P运动的路径=$\frac{120×π×2\sqrt{3}}{180}$=$\frac{4\sqrt{3}π}{3}$.
如图4所示:当AE=BF时.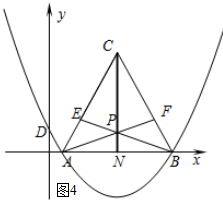
∵在△ABE和△BAF中$\left\{\begin{array}{l}{AE=FB}\\{∠EAB=∠FBA}\\{AB=BA}\end{array}\right.$,
∴△ABE≌△BAF.
∴AF=EB,∠FAB=∠EBA.
∴AP=BP.
∴点P在AB的垂直平分线上.
∴点P运动的路线=NC=3$\sqrt{3}$.
∴点P经过的路径长为$\frac{4\sqrt{3}π}{3}$或3$\sqrt{3}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法则求二次函数的解析式、等边三角形的性质、全等三角形的性质和判定、特殊锐角三角函数值,圆内接四边形的性质、圆周角定理、扇形的弧长公式、线段垂直平分线的判定,根据题意确定出点P运动的轨迹是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{2}{5}$ | D. | -$\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
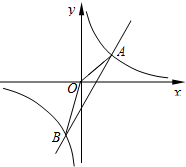 如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$的图象与一次函数y2=k2x+b的图象交于A、B两点,A(2,n),B(-$\frac{1}{2}$,-2).
如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$的图象与一次函数y2=k2x+b的图象交于A、B两点,A(2,n),B(-$\frac{1}{2}$,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2(a-1)=2a-1 | B. | (a+b)(b-a)=b2-a2 | C. | (a+1)2=a2+1 | D. | (-a-b)2=a2-2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 55°,55° | B. | 70°,40° | ||
| C. | 55°,55°或70°,40° | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
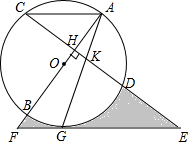 如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K、E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F.
如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K、E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com