
【题目】如图,把可以自由转动的圆形转盘A,B分别分成3等份的扇形区域,并在每一个小区域内标上数字.小明和小颖两个人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针两区域的数字均为奇数,则小明胜;若指针两区域的数字均为偶数,则小颖胜;若有指针落在分割线上,则无效,需重新转动转盘.这个游戏规则对双方公平吗?请说明理由.

科目:初中数学 来源: 题型:
【题目】某校1200名学生发起向贫困山区学生捐款活动,为了解捐款情况,学生会随机抽取了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②.
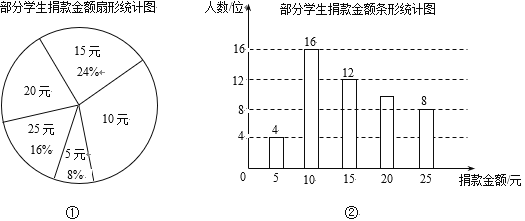
请根据以上信息,解答下列问题:
(1)本次抽样调查的样本容量为____;
(2)图①中“20元”对应扇形的圆心角的度数为_____°;
(3)估计该校本次活动捐款金额为15元以上(含15元)的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
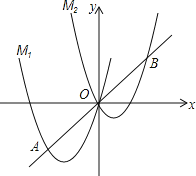
【题目】如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是﹣3.
(1)求a的值及M2的表达式;
(2)点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
①当点C的横坐标为2时,直线y=x+n恰好经过正方形CDEF的顶点F,求此时n的值;
②在点C的运动过程中,若直线y=x+n与正方形CDEF始终没有公共点,求n的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月1日是儿童节,为了迎接儿童节的到来,兰州某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
(3)在(2)条件下,若每件甲种玩具售价30元,每件乙种玩具售价45元,请求出卖完这批玩具获利W(元)与甲种玩具进货量m(件)之间的函数关系式,并求出最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
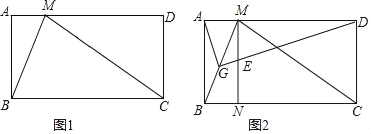
【题目】在矩形ABCD中,M为AD边上一点,MB平分∠AMC.
(1)如图1,求证:BC=MC;
(2)如图2,G为BM的中点,连接AG、DG,过点M作MN∥AB交DG于点E、交BC于点N.
①求证:AG⊥DG;
②当DGGE=13时,求BM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,如果一个矩形的宽与长之比为![]() ,那么这个矩形就称为黄金矩形.如图,已知A、B两点都在反比例函数y=
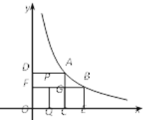
,那么这个矩形就称为黄金矩形.如图,已知A、B两点都在反比例函数y=![]() (k>0)位于第一象限内的图像上,过A、B两点分别作坐标轴的垂线,垂足分别为C、D和E、F,设AC与BF交于点G,已知四边形OCAD和CEBG都是正方形.设FG、OC的中点分别为P、Q,连接PQ.给出以下结论:①四边形ADFG为黄金矩形;②四边形OCGF为黄金矩形;③四边形OQPF为黄金矩形.以上结论中,正确的是( )
(k>0)位于第一象限内的图像上,过A、B两点分别作坐标轴的垂线,垂足分别为C、D和E、F,设AC与BF交于点G,已知四边形OCAD和CEBG都是正方形.设FG、OC的中点分别为P、Q,连接PQ.给出以下结论:①四边形ADFG为黄金矩形;②四边形OCGF为黄金矩形;③四边形OQPF为黄金矩形.以上结论中,正确的是( )
A. ①B. ②C. ②③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
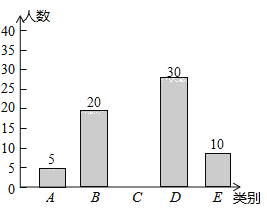
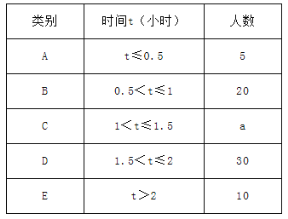
请根据图表信息解答下列问题:
(1)a=_____;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com