
【题目】已知关于x的方程mx2﹣(m+2)x+2=0
(1)求证:不论m为何值,方程总有实数根;
(2)若方程的一个根是2,求m的值及方程的另一个根.
【答案】(1)证明见解析(2)1,1
【解析】
试题分析:(1)分类讨论:当m=0时,方程为一元一次方程,有一个实数解;当m≠0时,计算判别式得到△=(m﹣2)2≥0,则方程有两个实数解,于是可判断不论m为何值,方程总有实数根;
(2)设方程的另一个根为t,利用根与系数的关系得到2+t=![]() ,2t=
,2t=![]() ,然后解关于t与m的方程组即可.
,然后解关于t与m的方程组即可.
试题解析:(1)证明:当m=0时,方程变形为﹣2x+2=0,解得x=1;
当m≠0时,△=(m+2)2﹣4m2=(m﹣2)2≥0,方程有两个实数解,
所以不论m为何值,方程总有实数根;
(2)设方程的另一个根为t,
根据题意得2+t=![]() ,2t=
,2t=![]() ,
,
则2+t=1+2t,解得t=1,
所以m=1,
即m的值位1,方程的另一个根为1.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:方程有两个不相等的实数根;
(2)设x1,x2为方程的两个实数根,且x1+2x2=14,试求出方程的两个实数根和k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
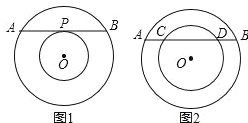
【题目】圆心相同,半径不相等的两个圆叫做同心圆,用大圆的面积减去小圆的面积就是圆环的面积.
(1)如图1,大圆的弦AB切小圆于点P,求证:AP=BP;
(2)若AB=2a,请用含有a的代数式表示图1中的圆环面积;
(3)如图2,若大圆的弦AB交小圆于C、D两点,且AB=8,CD=6,则圆环的面积为 ____ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
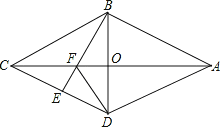
(1)证明:△CBF≌△CDF;
(2)若AC=2![]() ,BD=2,求四边形ABCD的周长;
,BD=2,求四边形ABCD的周长;
(3)请你添加一个条件,使得∠EFD=∠BAD,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分11分)学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
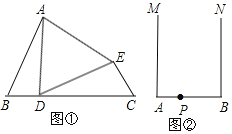
(1)如图①,∠B=∠C,BD=CE,AB=DC.
①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.
(2)如图②,射线AM与BN,AM⊥AB,BN⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点D满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com