
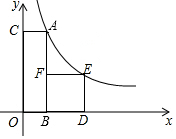
 如图,四边形ABOC是矩形,BDEF是正方形.点B、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点A、E在反比例函数y=$\frac{4t}{x}$的图象上,且AB=4AC,若正方形BDEF的面积为S,则S关于t的函数图象是( )
如图,四边形ABOC是矩形,BDEF是正方形.点B、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点A、E在反比例函数y=$\frac{4t}{x}$的图象上,且AB=4AC,若正方形BDEF的面积为S,则S关于t的函数图象是( )| A. | 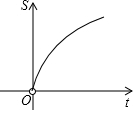 | B. | 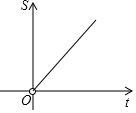 | C. |  | D. |  |
分析 首先求出A($\sqrt{t}$,4$\sqrt{t}$),再设BD=a,则E(a+$\sqrt{t}$,a),根据反比例函数图象上点的坐标特点可得(a+$\sqrt{t}$)a=4t,解方程求出a的值,代入S=a2,得出S关于t的函数解析式,进而求解即可.
解答 解:∵四边形ABOC是矩形,点A在反比例函数y=$\frac{4t}{x}$的图象上,且AB=4AC,
∴4t=AB•AC=4AC•AC,
∴AC=$\sqrt{t}$(负值舍去),
∴A($\sqrt{t}$,4$\sqrt{t}$).
设BD=a,
∵BDEF是正方形,
∴S=a2,E(a+$\sqrt{t}$,a),
∵点E在反比例函数y=$\frac{4t}{x}$的图象上,
∴(a+$\sqrt{t}$)a=4t,
整理,得a2+$\sqrt{t}$a-4t=0,
解得a=$\frac{-\sqrt{t}+\sqrt{17t}}{2}$(负值舍去),
∴S=a2=$\frac{1}{4}$(t-2$\sqrt{17}$t+17t)=$\frac{9-\sqrt{17}}{2}$t,
∴S是t的一次函数,
故选B.
点评 此题考查了反比例函数比例系数k的几何意义,反比例函数图象上点的坐标特点,反比例函数的图象与性质,得出S关于t的函数解析式是解题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
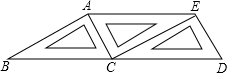 如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
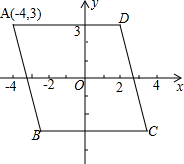 如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )
如图,菱形ABCD的中心是坐标原点,且AD∥x轴,点A的坐标为(-4,3),那么C点的坐标为( )| A. | (4,-3) | B. | (3,-4) | C. | (4,-4) | D. | (3,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
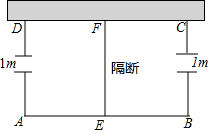 如图所示,利用一面墙(墙的长度足够),用篱笆围成一个形如矩形ABCD的场地,在AD,BC边上各有一个宽为1m的缺口,在场地中有用篱笆做的隔断EF,且EF⊥AB,AB>EF,已知所用篱笆总长度为38m.
如图所示,利用一面墙(墙的长度足够),用篱笆围成一个形如矩形ABCD的场地,在AD,BC边上各有一个宽为1m的缺口,在场地中有用篱笆做的隔断EF,且EF⊥AB,AB>EF,已知所用篱笆总长度为38m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com