
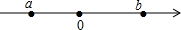 设实数a、b在数轴上对应位置如图所示,化简:$\sqrt{{a}^{2}}$+|a+b|的结果是b.
设实数a、b在数轴上对应位置如图所示,化简:$\sqrt{{a}^{2}}$+|a+b|的结果是b. 分析 首先根据数轴的特征,可得a<0<b,而且a+b>0;然后分别求出$\sqrt{{a}^{2}}$、|a+b|的值是多少,再把它们求和,求出$\sqrt{{a}^{2}}$+|a+b|的结果是多少即可.
解答 解:根据数轴的特征,可得
a<0<b,而且a+b>0,
∴$\sqrt{{a}^{2}}$+|a+b|
=-a+a+b
=b
故答案为:b.
点评 (1)此题主要考查了实数与数轴,要熟练掌握,解答此题的关键是要明确:实数与数轴上的点是一一对应关系.任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.数轴上的任一点表示的数,不是有理数,就是无理数.
(2)此题还考查了二次根式的性质和化简,注意算术平方根的非负性质,以及绝对值的非负性质的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
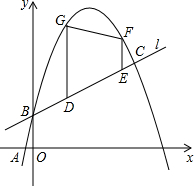 如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).
如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
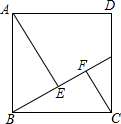 如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.
如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.
如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com