
【题目】如图,在正方形![]() 中,以
中,以![]() 为边作等边
为边作等边![]() ,延长
,延长![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]()
![]() 与
与![]() 相交于点
相交于点![]() ,给出下列结论: ①
,给出下列结论: ①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的是( )
;其中正确的是( )
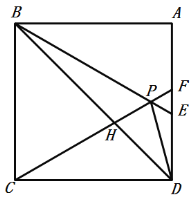
A.①②③④B.②③C.①②④D.①③④
【答案】A
【解析】
根据等边三角形、正方形的性质求得∠ABE=30°,利用直角三角形中30°角的性质即可判断①;证得PC=CD,利用三角形内角和定理即可求得∠PDC,可求得∠BPD,即可判断②;求得∠FDP=15°,∠PBD=15°,即可证明△PDE∽△DBE,判断③正确;利用相似三角形对应边成比例可判断④.
∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴![]() ,
,
∴![]() ;故①正确;
;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=∠CPD =![]() =
=![]() =75°,
=75°,
∴∠BPD=∠BPC+ ∠CPD =60°+75°=135°,故②正确;
∵∠PDC=75°,
∴∠FDP=∠ADC -∠PDC=90°- 75°=15°,
∵∠DBA=45°,
∴∠PBD=∠DBA -∠ABE =45°-30°=15°,
∴∠EDP=∠EBD,
∵∠DEP=∠DEP,
∴△PDE∽△DBE,故③正确;
∵△PDE∽△DBE,
∴![]() ,即
,即![]() ,故④正确;
,故④正确;
综上:①②③④都是正确的.
故选:A.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
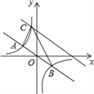
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一般的,如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.——苏科版《数学》九年级(下册)P21”参考上述教材中的话,判断方程x2﹣2x=![]() ﹣2实数根的情况是 ( )
﹣2实数根的情况是 ( )
A. 有三个实数根 B. 有两个实数根 C. 有一个实数根 D. 无实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有2000名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
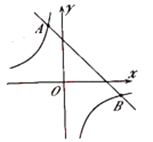
(1)根据图象,直接写出满足![]() 的
的![]() 的取值范围;
的取值范围;
(2)求这两个函数的表达式;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
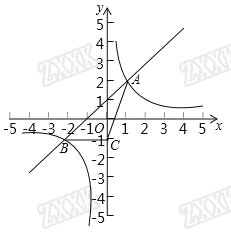
【题目】如图,反比例函数![]() 的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和﹣2,这两点的纵坐标之和为1.
的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和﹣2,这两点的纵坐标之和为1.
(1)求反比例函数的表达式与一次函数的表达式;
(2)当点C的坐标为(0,﹣1)时,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com