
【题目】若四边形的一条对角线把四边形分成两个等腰三角形,则这条对角线叫做这个四边形的“巧分线”,这个四边形叫“巧妙四边形”,若一个四边形有两条巧分线,则称为“绝妙四边形”.
(1)下列四边形一定是巧妙四边形的是 ;(填序号点①平行四边形;②矩形;③菱形;④正方形.
初步应用
(2)在绝妙四边形ABCD中,AC垂直平分BD,若∠BAD=80°,则∠BCD= ;
深入研究
(3)如图,在梯形ABCD中,AD∥BC,AB=AD=CD,∠B=72°.求证:梯形ABCD是绝妙四边形.
(4)在巧妙四边形ABCD中,AB=AD=CD,∠A=90°,AC是四边形ABCD的巧分线,请直接写出∠BCD的度数.

【答案】(1)③④;(2)140°或80°或160°;(3)见解析;(4)∠BCD的度数是45°或135°或90°
【解析】
(1)由巧妙四边形的定义,即可得到菱形和正方形是巧妙四边形;
(2)根据绝妙四边形的定义可知:两条对角线都是巧分线,分情况画图进行计算可得结论;
(3)首先根据题意画出图形,然后分别证明两条对角线分成的三角形是等腰三角形即可;
(4)根据AC是四边形ABCD的巧分线,可知:△ACD和△ABC是等腰三角形,△ABC是等腰三角形时分三种情况画图进行讨论可得结论.
解:(1)∵菱形的四条边相等,
∴连接对角线能得到两个等腰三角形,
∴菱形是巧妙四边形;
正方形是特殊的菱形,所以正方形也是巧妙四边形;
故答案是:③④;
(2)分三种情况,
①当AC=AD=AB时,如图1,
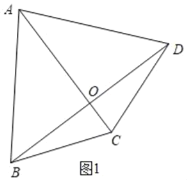
∵AC垂直平分BD,
∴AB=AD,BC=CD,AC⊥BD,
∴∠BAC=∠DAC,
∵∠BAD=80°,
∴∠BAC=∠DAC=40°,
∵AC=AD=AB,
∴∠ACD=∠ADC=∠ACB=∠ABC=![]() =70°,
=70°,
∴∠BCD=2∠ACD=140°;
②当AD=CD,AB=BC时,如图2,
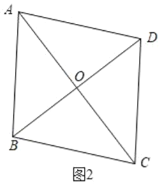
∵AC垂直平分BD,
∴AB=AD,BC=CD,AC⊥BD,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形,
∴∠BCD=∠BAD=80°;
③在四边形ABCD中,AC=CD=BC,如图3,
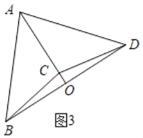
∴∠CAD=∠ADC=40°
∴∠ACD=∠ACB=100°
∴∠BCD=360°﹣100°﹣100°=160°;
综上,∠BCD=140°或80°或160°;
故答案为:140°或80°或160°;
(3)如图4,连接AC与BD,交于点O,
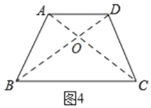
在梯形ABCD中,AB=CD,
∴∠ABC=∠DCB=72°,
∵AD∥BC,
∴∠BAD=∠ADC=108°,
∵AB=AD=CD,
∴△ABD是等腰三角形,∠ABD=∠ADB=36°,
∴∠DBC=72°﹣36°=36°,∠BDC=108°﹣36°=72°=∠DCB,
∴△BDC也是等腰三角形,
∴对角线BD叫做这个四边形ABCD的“巧分线”,
同理可得△ADC和△ACB也是等腰三角形,
∴对角线AC叫做这个四边形ABCD的“巧分线”,
∴梯形ABCD是绝妙四边形;
(4)∵AC是四边形ABCD的巧分线,
∴△ACD和△ABC是等腰三角形,
①当AC=BC时,如图5,过C作CH⊥AB于H,过C作CG⊥AD,交AD的延长线于G,
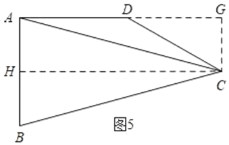
∵∠HAD=∠AHC=∠G=90°,
∴四边形AHCG是矩形,
∴AH=CG=![]() AB=
AB=![]() CD,
CD,
∴∠CDG=30°,
∴∠ADC=150°,
∴∠DAC=∠DCA=15°,
∵∠DAB=90°,
∴∠CAB=∠B=75°,
∴∠ACB=30°,
∴∠BCD=30°+15°=45°;
②当AC=AB时,如图6,

∵AC=AB=AD=CD,
∴△ACD是等边三角形,
∴∠CAD=∠ACD=60°,
∵∠BAD=90°,
∴∠BAC=30°,
∵AB=AC,
∴∠ACB=75°,
∴∠BCD=75°+60°=135°;
③当AB=BC时,如图7,此时∠BCD=90°
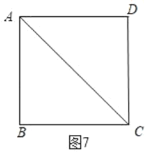
综上,∠BCD的度数是45°或135°或90°.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
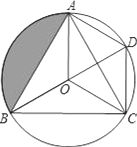
【题目】如图,O是等边△ABC的外心,BO的延长线和⊙O相交于点D,连接DC,DA,OA,OC.
(1)求证:△BOC≌△CDA;
(2)若AB=![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填“变大”、“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2( ),
且∠1=∠4( )
∴∠2=∠4(等量代换)
∴CE∥BF( )
∴∠ =∠3( )
又∵∠B=∠C(已知)
∴∠3=∠B( )
∴AB∥CD( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与证明:
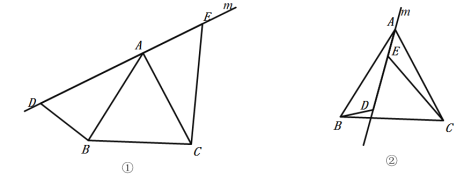
(1)如图①,直线![]() 经过正三角形
经过正三角形![]() 的顶点
的顶点![]() ,在直线
,在直线![]() 上取点
上取点![]() ,
,![]() ,使得
,使得![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明;
之间满足的数量关系,并予以证明;
(2)将(1)中的直线![]() 绕着点
绕着点![]() 逆时针方向旋转一个角度到如图②的位置,
逆时针方向旋转一个角度到如图②的位置,![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明.
之间满足的数量关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
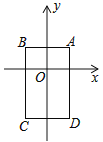
【题目】如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
A. (﹣1,﹣2) B. (―1,1)
C. (-1,-1) D. (1,―2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com