练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．已知一元二次方程x2-6x+4=0的两根分别是a，b，求
    （1）a2+b2
    （2）a2-b2的值．

    分析 根据根与系数的关系找出a+b=6，ab=4．
    （1）将a2+b2变成只含a+b和ab的代数式，代入数据即可得出结论；
    （2）将a2-b2变成只含a+b和ab的代数式，代入数据即可得出结论．

    解答 解：∵方程x2-6x+4=0的两根分别是a，b，
    ∴a+b=6，ab=4．
    （1）a2+b2=（a+b）2-2ab=62-2×4=28．
    （2）a2-b2=（a+b）2-4ab=62-4×4=20．

    点评 本题考查了根与系数的关系，解题的关键是：（1）将a2+b2变成（a+b）2-2ab；（2）将a2-b2变成（a+b）2-4ab．本题属于基础题，难度不大，解决该题型题目时，根据根与系数的关系找出两根之和与两根之积是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

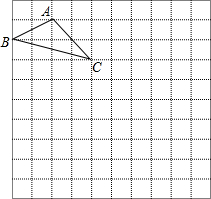    2．如图，△ABC的顶点都在方格纸的格点上，将△ABC向右平移4格，再向下平移3格，其中每个格子的边长为1个单位长度．
    （1）请在图中画出平移后的△A′B′C′；
    （2）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．用适当方法解下列方程
    （1）x2+4x+1=0                   
    （2）x（x+2）=-1
    （3）x（x-2）=2-x                 
    （4）（2x+1）2=x+2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，直线y=x+3与双曲线y=$\frac{m-3}{x}$（ m为常数）交于点A（a，2）、B两点．
    （1）求a、m的值和B点坐标；
    （2）双曲线y=$\frac{m-3}{x}$上有三点M（x1，y1）、N（x2，y2）、P（x3，y3），且y1＜y2＜0＜y3，则x1、x2、x3的大小关系是x3＜x1＜x2（用“＜”号连接）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知函数y=ax${\;}^{{a}^{2}-2a+2}$+（a-2）x，若它是二次函数，则a=2，函数的表达式是y=2x2其图象是一条抛物线，位于第一、二象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某地政府计划为农户购买农机设备提供补贴．其中购买Ⅰ型、Ⅱ型设备农民所投资的金额与政府补贴的额度存在下表所示的函数对应关系．

    型号
    金额    		Ⅰ型设备Ⅱ型设备
    投资金额x（万元）x5x24
    补贴金额y（万元）y1=kx（k≠0）2y2=ax2+bx（a≠0）2.84
    （1）分别求y1和y2的函数解析式；
    （2）有一农户共投资10万元购买Ⅰ型、Ⅱ型两种设备，两种设备的投资均为整数万元，要想获得最大补贴金额，应该如何购买？能获得的最大补贴金额为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，⊙O的直径AB⊥弦CD，垂足为点E，点P在优弧CAD上（不包含点C和点D），连PC、PD、CB，tan∠BCD=$\frac{1}{2}$
    （1）求证：AE=CD；
    （2）求sin∠CPD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算（3ab-7）•（-4a2+6ab+7）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．某市为鼓励居民节约用水，规定如下用水收费标准：每户每月的用水量不超过12吨（含12吨）时，水费按a元/吨收费；超过时，不超过12吨（含12吨）时，水费按a元/吨收费；超过时，不超过12吨的部分仍按a元/吨收费，超过的部分按b元/吨（b＞a）收费，已知该市小明家今年3月份和4月份的用水量、水费如表所示：
    月份用水量（立方米）水费（元）
    32856
    42035.2
    （1）求a，b的值；
    （2）设某户1个月的用水量为x（吨），应交水费y（元），求出y与x之间的函数关系式；
    （3）已知某户5月份的用水量为18吨，求该户5月份的水费．

    查看答案和解析>>

    同步练习册答案